题目内容
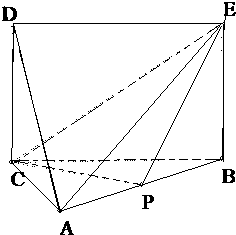 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
(1)求证:AD∥平面PCE;
(2)求二面角A-CE-P的余弦值.
分析:(1)连接BD交CE于点Q,连接PQ,可得PQ是△ABD的中位线,得PQ∥AD,结合线面平行判定定理可得AD∥平面PCE;
(2)过点P作PF⊥AE于F,再过点F作FG⊥EC于G,连接PG.根据线面垂直的判定与性质,可得PG⊥EC,得∠PGF就是二面角A-CE-P的平面角.Rt△PFG中,算出FG、PG的长,可得cos∠PGF=
=
,即二面角A-CE-P的余弦值.
(2)过点P作PF⊥AE于F,再过点F作FG⊥EC于G,连接PG.根据线面垂直的判定与性质,可得PG⊥EC,得∠PGF就是二面角A-CE-P的平面角.Rt△PFG中,算出FG、PG的长,可得cos∠PGF=
| GF |
| PG |
17
| ||
| 793 |
解答:解:(1)连接BD交CE于点Q,连接PQ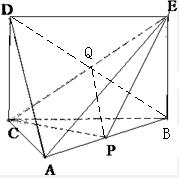
∵EB∥DC,DC=EB,∴四边形BCDE是平行四边形,得Q为BD中点
由此可得△ABD中,PQ是中位线,可得PQ∥AD
∵PQ?平面PCE,AD?平面PCE,
∴AD∥平面PCE;…(6分)
(2)过点P作PF⊥AE于F,再过点F作FG⊥EC于G,连接PG
∵DC⊥平面ABC,EB∥DC,
∴EB⊥平面ABC,结合AC?平面ABC,得AC⊥EB
∵AC⊥AB,AB∩EB=B,∴AC⊥平面ABE
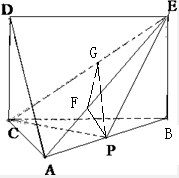 ∵PF?平面ABE,∴AC⊥PF
∵PF?平面ABE,∴AC⊥PF
∵AE⊥PF,AC∩AE=A,∴PF⊥平面ACE
∵FG⊥EC,FG是PG在平面ACE内的射影
∴PG⊥EC,得∠PGF就是二面角A-CE-P的平面角
∵Rt△ABE中,AB=3,BE=2,P为AB中点,且PF⊥AE
∴由△ABE∽△AFP,得PF=
同理:由△ACE∽△FGE,得GF=
∴Rt△PFG中,PG=
=
因此,cos∠PGF=
=
,即二面角A-CE-P的余弦值等于
.…(12分)

∵EB∥DC,DC=EB,∴四边形BCDE是平行四边形,得Q为BD中点
由此可得△ABD中,PQ是中位线,可得PQ∥AD
∵PQ?平面PCE,AD?平面PCE,
∴AD∥平面PCE;…(6分)
(2)过点P作PF⊥AE于F,再过点F作FG⊥EC于G,连接PG
∵DC⊥平面ABC,EB∥DC,
∴EB⊥平面ABC,结合AC?平面ABC,得AC⊥EB
∵AC⊥AB,AB∩EB=B,∴AC⊥平面ABE
 ∵PF?平面ABE,∴AC⊥PF
∵PF?平面ABE,∴AC⊥PF∵AE⊥PF,AC∩AE=A,∴PF⊥平面ACE
∵FG⊥EC,FG是PG在平面ACE内的射影
∴PG⊥EC,得∠PGF就是二面角A-CE-P的平面角
∵Rt△ABE中,AB=3,BE=2,P为AB中点,且PF⊥AE
∴由△ABE∽△AFP,得PF=
3
| ||
| 13 |
同理:由△ACE∽△FGE,得GF=
| 17 | ||
2
|
∴Rt△PFG中,PG=
| PF2+FG2 |
| ||
2
|
因此,cos∠PGF=
| GF |
| PG |
17
| ||
| 793 |
17
| ||
| 793 |
点评:本题在特殊多面体中,证明线面平行并且求二面角的余弦值,着重考查了直线与平面平行的判定,二面角的平面角的定义及求法等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
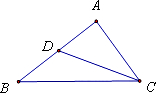 如图所示,在△ABC中,点D是边AB的中点,则向量
如图所示,在△ABC中,点D是边AB的中点,则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
 如图所示,在△ABC,已知
如图所示,在△ABC,已知 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD= 如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则
如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=