题目内容
10.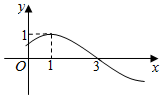 函数y=sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图,则该函数的解析式为y=sin($\frac{π}{4}$x$+\frac{π}{4}$).
函数y=sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图,则该函数的解析式为y=sin($\frac{π}{4}$x$+\frac{π}{4}$).
分析 根据三角函数的图象和性质可得函数的周期为8,从而求出ω,将(1,1)代入函数解析式求出φ,得出函数的解析式.
解答 解:偶函数图象可知函数y=sin(ωx+φ)的周期T=4×(3-1)=8.
∵ω>0,∴T=$\frac{2π}{ω}=8$,解得ω=$\frac{π}{4}$.
由函数图象可知当x=1时,函数值为1.
故sin($\frac{π}{4}$+φ)=1,∴$\frac{π}{4}+$φ=$\frac{π}{2}+2kπ$,解得φ=$\frac{π}{4}$+2kπ.
∵-π<φ<π,∴φ=$\frac{π}{4}$.
故答案为y=sin($\frac{π}{4}x+\frac{π}{4}$).
点评 本题考查了三角函数的图象与性质,根据函数图象得出函数周期是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
1.给出下面的程序框图,则输出的结果为( )
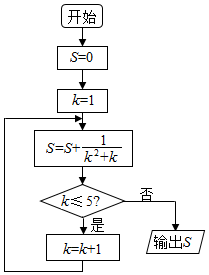

| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{6}{7}$ |