题目内容

20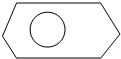．如图，在一个不规则多边形内随机撒入200粒麦粒（麦粒落到任何位置可能性相等），恰有40粒落入半径为1的圆内，则该多边形的面积约为（　　）
A．4πB．5πC．6πD．7π

分析 由几何概型概率计算公式，以面积为测度，可求该阴影部分的面积．

解答 解：设该多边形的面积为S，则$\frac{40}{200}=\frac{π•{1}^{2}}{S}$，
∴S=5π，
故选：B．

点评 本题考查概率的性质和应用，每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概型． 解题时要认真审题，合理地运用几何概型解决实际问题．

练习册系列答案
相关题目
20．已知集合A=（-∞，3），B=（1，+∞），求A∪B，A∩B．
1．一种产品原来成本为1万元，在今后几年内计划成本平均每年降低6%，求大约经过几年成本价降为原来的一半？（lg2≈0.3010，lg0.94≈-0.0269）
8．判断函数奇偶性：f（x）=lg（$\sqrt{1+{x}^{2}}$+x）．
15．设a，b，c∈R+，求证：a+b+c≤$\frac{{a}^{2}+{b}^{2}}{2c}$+$\frac{{b}^{2}+{c}^{2}}{2a}$+$\frac{{c}^{2}+{a}^{2}}{2b}$≤$\frac{{a}^{3}}{bc}$+$\frac{{b}^{3}}{ca}$+$\frac{{c}^{3}}{ab}$．
5．数列$\left\{{tan\frac{n}{9}π•tan\frac{n+1}{9}π}\right\}$的前n项和记为Sn，则S2015=（　　）
A．-2016B．-2015C．-2014D．-1007
12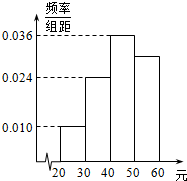．学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n且支出在[20，60）元的样本，其频率分布直方图如图所示，根据此图估计学生在课外读物方面的支出费用的中位数为（　　）元．
A．45B．46C．$\frac{390}{9}$D．$\frac{400}{9}$
9．某程序框图如图所示，当输出y值为-8时，则输出x的值为（　　）
A．64B．32C．16D．8
10．已知点 P（3，4），Q（2，6），向量$\overrightarrow{{E}F}=（{-1，λ}）$．若$\overrightarrow{{P}Q}∥\overrightarrow{{E}F}$，则实数λ的值为（　　）
A．$\frac{1}{2}$B．2C．$-\frac{1}{2}$D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网