题目内容
如图所示,在三棱锥A—BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD= ,BD=CD=1,另一个侧面ABC是正三角形.
,BD=CD=1,另一个侧面ABC是正三角形.

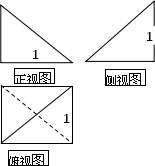
(1)当正视图方向与向量 的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)
的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)
(2)求二面角B—AC—D的余弦值;
(3)在线段AC上是否存在一点E,使ED与平面BCD成30°角? 若存在,确定点E的位置;若不存在,说明理由.
 ,BD=CD=1,另一个侧面ABC是正三角形.
,BD=CD=1,另一个侧面ABC是正三角形.
(1)当正视图方向与向量
 的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)
的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)(2)求二面角B—AC—D的余弦值;
(3)在线段AC上是否存在一点E,使ED与平面BCD成30°角? 若存在,确定点E的位置;若不存在,说明理由.
(1)详见解析;(2)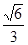 ;(3)存在且
;(3)存在且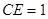
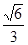 ;(3)存在且
;(3)存在且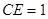
试题分析:(1)画三视图时要注意:正视图看到的是几何体的长和高,侧视图看到的是几何体的宽和高,俯视图看到的是几何体的长和宽,同时要想象自己身处教室,前面、右面、地面有墙,将几何体正投影到这三个方向;(2)建立适当的空间直角坐标系,需选择两两垂直的三条直线,然后把涉及到的点用坐标表示,如图所示建立坐标系,则
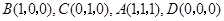 ,求出面
,求出面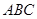 和面
和面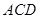 的法向量,然后求法向量的夹角,进而求出二面角的余弦值;(3)利用空间直角坐标系求直线和平面所成的角,先求平面的法向量和直线方向向量夹角的余弦值,即直线和平面所成角的正弦值,该题利用三点共线,可设出点
的法向量,然后求法向量的夹角,进而求出二面角的余弦值;(3)利用空间直角坐标系求直线和平面所成的角,先求平面的法向量和直线方向向量夹角的余弦值,即直线和平面所成角的正弦值,该题利用三点共线,可设出点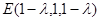 ,然后计算
,然后计算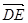 和平面
和平面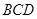 法向量,根据它们夹角余弦值等于
法向量,根据它们夹角余弦值等于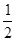 列式,求
列式,求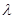 .
.试题解析:(1) 三棱锥A—BCD的三视图如右图所示:
(2)以
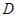 为坐标原点,分别以
为坐标原点,分别以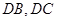 和过点
和过点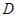 垂直于面
垂直于面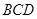 的直线为
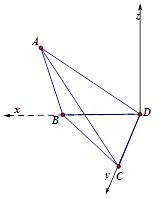
的直线为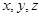 轴,建立如图所示的空间直角坐标系,则
轴,建立如图所示的空间直角坐标系,则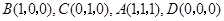 设平面ABC的法向量为
设平面ABC的法向量为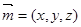 ,,则
,,则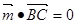
且
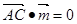 ,∴
,∴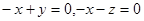 ,令
,令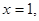 则
则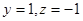 ,则
,则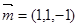 ,同理,可求得平面ACD的一个法向量为
,同理,可求得平面ACD的一个法向量为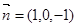 ,所以
,所以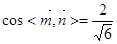 =
=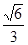 .所以二面角B—AC—D的余弦值
.所以二面角B—AC—D的余弦值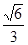 ;
;
(3)设
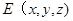 ,由
,由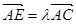 ,得
,得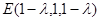 ,面
,面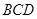 的一个法向量
的一个法向量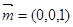 ,
,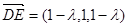 ,所以
,所以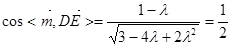 ,解得
,解得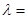
 ,所以存在
,所以存在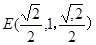 ,即
,即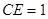 时,ED与平面BCD成30°角.
时,ED与平面BCD成30°角.
练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目









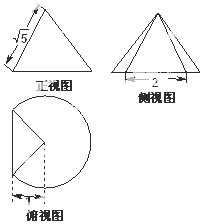

 +1
+1



 ,用斜二测画法画出它的直观图
,用斜二测画法画出它的直观图 如图所示,此直观图恰好是一个边长为
如图所示,此直观图恰好是一个边长为 的正方形,则原平面图形
的正方形,则原平面图形
