题目内容
如图所示，在正方体ABCD-A1B1C1D1中，E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点，N是BC的中点，点M在四边形EFGH及其内部运动，则M满足考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：根据平面FHN∥平面B1BDD1，可知平面FHN内任意一条直线都与平面B1BDD1平行，而点M在四边形EFGH上及其内部运动，所以M满足条件M∈FH．
解答：
解：∵HN∥DB，FH∥D1D，
∴面FHN∥面B1BDD1．
∵点M在四边形EFGH上及其内部运动
故M∈FH．
故答案为：M∈FH
∴面FHN∥面B1BDD1．
∵点M在四边形EFGH上及其内部运动
故M∈FH．
故答案为：M∈FH
点评：本题主要考查了直线与平面平行的判定、面面平行的性质，考查学生空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
口算能手系列答案
相关题目
按照程序框图执行，第3个输出的数是（ ）
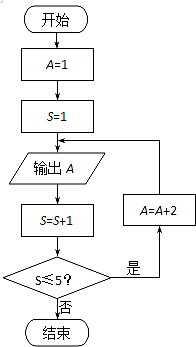
| A、4 | B、5 | C、6 | D、7 |
已知复数z1=1+i，z2=
在复平面内对应的点分别为P1、P2，O为坐标原点，则向量
、
所成的角为（ ）
| 1 |
| 1+i |
| OP1 |
| OP2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
九个人排成三行三列的方阵，从中任选三人，则至少有两人位于同行或同列的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
过双曲线
-
=1，（a＞0，b＞0）的右焦点F作垂直于x轴的直线，交双曲线的渐近线于A、B两点，若△OAB（O为坐标原点）是等边三角形，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
若x∈A，
∈A，则称A是“伙伴关系集合”，在集合M={-1， 0，
，
，1， 2， 3， 4}的所有非空子集任选一个集合，则该集合是“伙伴关系集合”的概率为（ ）
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|