题目内容
过点(4,1)的直线l与x轴的正半轴,y轴正半轴分别交于A、B两点,当OA+OB最小时,求直线l的方程.
考点:基本不等式,直线的截距式方程
专题:不等式的解法及应用,直线与圆
分析:设出直线的截距式方程,可得有
+
=1,进而可得OA+OB=a+b=(a+b)(
+
)=5+
+
,由基本不等式可得.
| 4 |
| a |
| 1 |
| b |
| 4 |
| a |
| 1 |
| b |
| 4b |
| a |
| a |
| b |
解答:
解:设OA=a,OB=b,则l方程可设为
+
=1(a>0,b>0),
又l过点(4,1),∴有
+
=1
故OA+OB=a+b=(a+b)(
+
)=5+
+
≥9
当且仅当
=
即a=2b时取等号,
结合
+
=1 可解得a=6,b=3
∴l方程为
+
=1,
化为一般式可得:x+2y-6=0…(14分)
| x |
| a |
| y |
| b |
又l过点(4,1),∴有
| 4 |
| a |
| 1 |
| b |
故OA+OB=a+b=(a+b)(
| 4 |
| a |
| 1 |
| b |
| 4b |
| a |
| a |
| b |
当且仅当
| 4b |
| a |
| a |
| b |
结合
| 4 |
| a |
| 1 |
| b |
∴l方程为
| x |
| 6 |
| y |
| 3 |
化为一般式可得:x+2y-6=0…(14分)
点评:本题考查直线的截距式方程,涉及基本不等式,属基础题.

练习册系列答案
相关题目
若α的终边经过点P(3,-4),则tan(α+
)=( )
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
等比数列{an}中,已知a3=1,a7=4,则a5=( )
| A、-1 | B、2 | C、±2 | D、不能确定 |
下列各组两个集合M和N,表示同一集合的是( )
| A、M={π},N={3.14159} |
| B、M={2,3},N={(2,3)} |
| C、M={(x,y)|x+y=1},N={y|x+y=1} |
| D、M={x|x2+1=0},N=∅ |

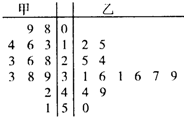 某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,用茎叶图分别记录抽查数据如下:
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,用茎叶图分别记录抽查数据如下: