题目内容
已知R上的连续函数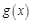 满足:①当
满足:①当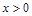 时,
时,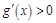 恒成立(
恒成立(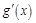 为函数
为函数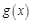 的导函数);②对任意
的导函数);②对任意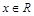 都有
都有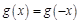 。又函数
。又函数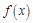 满足:对任意的
满足:对任意的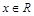 都有
都有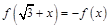 成立,当
成立,当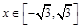 时,
时,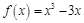 。若关于x的不等式
。若关于x的不等式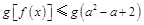 对
对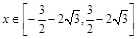 恒成立,则a的取值范围是( )
恒成立,则a的取值范围是( )
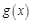 满足:①当
满足:①当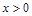 时,
时,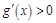 恒成立(
恒成立(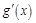 为函数
为函数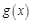 的导函数);②对任意
的导函数);②对任意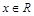 都有
都有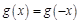 。又函数
。又函数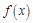 满足:对任意的
满足:对任意的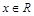 都有
都有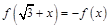 成立,当
成立,当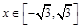 时,
时,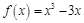 。若关于x的不等式
。若关于x的不等式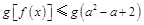 对
对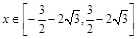 恒成立,则a的取值范围是( )
恒成立,则a的取值范围是( )A. 或 或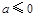 | B.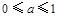 |
C.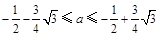 ? ? | D.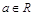 |
A
因为对任意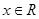 都有
都有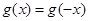 ,所以
,所以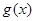 为偶函数。而当
为偶函数。而当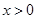 时,
时,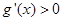 恒成立,即
恒成立,即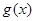 单调递增,所以当
单调递增,所以当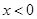 时,
时,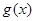 单调递减。
单调递减。
因为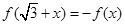 ,所以
,所以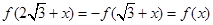 ,即
,即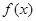 是周期为
是周期为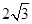 的周期函数,所以当
的周期函数,所以当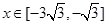 时,
时,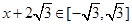 ,则
,则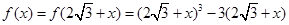 。
。
因为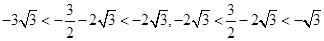
所以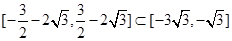
所以此时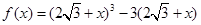 ,则
,则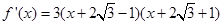 ,此时当
,此时当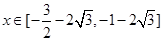 或
或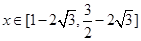 时,
时,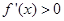 ,
,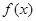 单调递增,当
单调递增,当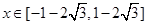 时,
时,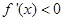 ,
,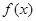 单调递减。
单调递减。
而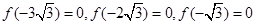
所以当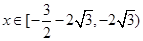 时,
时,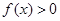 且
且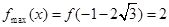 ,则此时不等式
,则此时不等式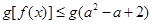 等价于
等价于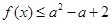 恒成立,所以
恒成立,所以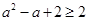 ,解得
,解得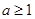 或
或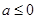
当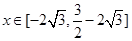 时,
时,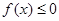 且
且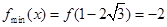 ,则此时不等式
,则此时不等式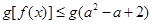 等价于
等价于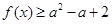 恒成立,所以
恒成立,所以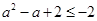 ,此时无解。
,此时无解。
综上可得,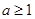 或
或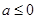 ,故选A
,故选A
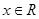 都有
都有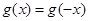 ,所以
,所以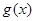 为偶函数。而当
为偶函数。而当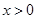 时,
时,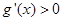 恒成立,即
恒成立,即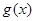 单调递增,所以当
单调递增,所以当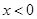 时,
时,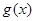 单调递减。
单调递减。因为
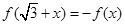 ,所以
,所以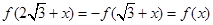 ,即
,即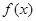 是周期为
是周期为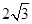 的周期函数,所以当
的周期函数,所以当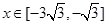 时,
时,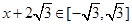 ,则
,则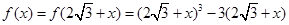 。
。因为
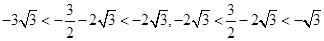
所以
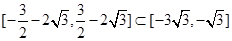
所以此时
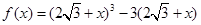 ,则
,则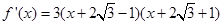 ,此时当
,此时当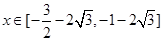 或
或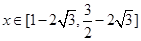 时,
时,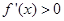 ,
,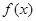 单调递增,当
单调递增,当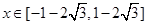 时,
时,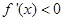 ,
,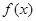 单调递减。
单调递减。而
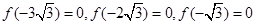
所以当
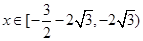 时,
时,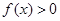 且
且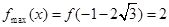 ,则此时不等式
,则此时不等式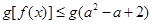 等价于
等价于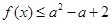 恒成立,所以
恒成立,所以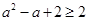 ,解得
,解得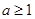 或
或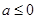
当
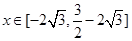 时,
时,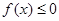 且
且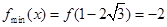 ,则此时不等式
,则此时不等式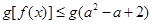 等价于
等价于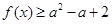 恒成立,所以
恒成立,所以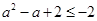 ,此时无解。
,此时无解。综上可得,
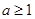 或
或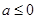 ,故选A
,故选A
练习册系列答案
相关题目
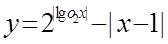 的图象大致是
的图象大致是 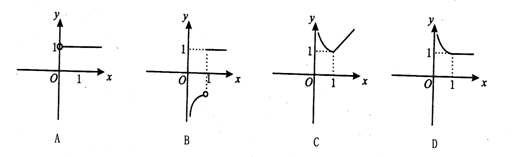
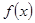 的导函数为
的导函数为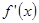 ,且满足
,且满足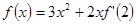 ,则
,则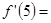
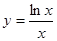 的最大值为( )
的最大值为( )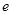
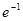
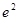
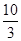
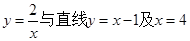 所围成的封闭图形的面积为
所围成的封闭图形的面积为 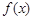 是定义在
是定义在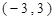 上的奇函数,当
上的奇函数,当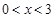 时,
时,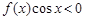 的解集是
的解集是 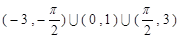
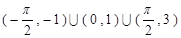
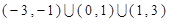
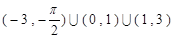
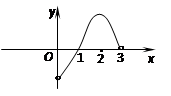
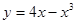 在点(-1,-3)处的切线方程是 ( ▲ )
在点(-1,-3)处的切线方程是 ( ▲ )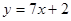
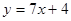
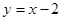
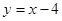
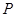 在曲线
在曲线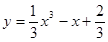 上移动,若经过点
上移动,若经过点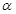 ,则
,则