题目内容
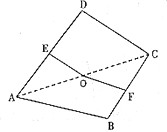
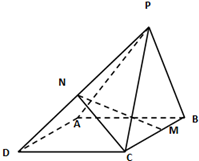
如图,已知ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,PA=2,PD=AB,且平面MND⊥平面PCD.
(1)求证:MN⊥AB;
(2)求二面角P-CD-A的大小;
(3)求三棱锥D-AMN的体积.
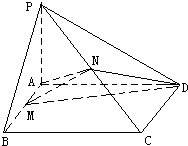
(1)求证:MN⊥AB;
(2)求二面角P-CD-A的大小;
(3)求三棱锥D-AMN的体积.

(1)∵PA⊥面ABCD,ABCD是矩形
∴∠PAC=∠PBC=90°…(2分)
又N为PC的中点,∴AN=
PC,BN=
PC
∴AN=BN…(4分)
而M是AB的中点,∴MN⊥AB…(5分)
(2)由PD=AB=DC,N是PC的中点得:ND⊥PC,
又由面MND⊥面PCD得:PC⊥面MND
∴PC⊥MN∴MP=MC…(7分)
Rt△MPA≌Rt△MCB,
∴PA=BC=2
即PA=AD=2,∠PDA=45°,…(9分)
易知∠PDA为二面角P-CD-A的平面角
∴二面角P-CD-A的大小为45°…(10分)
(3)N到平面AMD的距离d=1,AM=
,AD=2…(12分)
所以VD-AMN=VN-AMD=
d•S△AMD=
d•(
•AM•AD)=
…(14分)
∴∠PAC=∠PBC=90°…(2分)
又N为PC的中点,∴AN=
| 1 |
| 2 |
| 1 |
| 2 |
∴AN=BN…(4分)
而M是AB的中点,∴MN⊥AB…(5分)
(2)由PD=AB=DC,N是PC的中点得:ND⊥PC,
又由面MND⊥面PCD得:PC⊥面MND
∴PC⊥MN∴MP=MC…(7分)
Rt△MPA≌Rt△MCB,
∴PA=BC=2
即PA=AD=2,∠PDA=45°,…(9分)
易知∠PDA为二面角P-CD-A的平面角
∴二面角P-CD-A的大小为45°…(10分)
(3)N到平面AMD的距离d=1,AM=
| 2 |
所以VD-AMN=VN-AMD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |

练习册系列答案
相关题目