Question

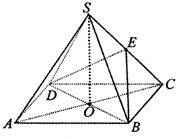
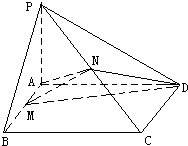
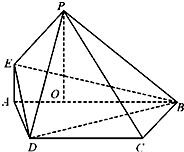
如图，已知PO⊥平面ABCD，点O在AB上，EA∥PO，四边形ABCD是直角梯形，AB∥DC，且BC⊥AB，BC=CD=BO=PO，EA=AO=

1

2

CD．
（Ⅰ）求证：PE⊥平面PBC；
（Ⅱ）求二面角C-PB-D的大小；
（Ⅲ）在线段PE上是否存在一点M，使DM∥平面PBC，若存在求出点M；若不存在，说明理由．

Answer 1

证明：（Ⅰ）连接DO，BO∥CD且BO=CD，则四边形BODC是平行四边形，
故BC∥OD，又BC⊥AB，则BO⊥OD，因为PO⊥平面ABCD，
可知OD、OB、OP两两垂直，分别以OD、OB、OP为x、y、z轴建立空间直角坐标系．
设AO=1，则B（0，2，0），C（2，2，0），D（2，0，0），E（0，-1，1），P（0，0，2），
则

PE

=(0，-1，-1)，

PB

=(0，2，-2)，

BC

=(2，0，0)．
则

PE

•

PB

=0，

PE

•

BC

=0，故PE⊥PB，PE⊥BC，又PB∩BC=B，
∴PE⊥平面PBC．
（Ⅱ）由（Ⅰ）可知，平面PBC的一个法向量

n1

=

PE

=(0，-1，-1)，设面PBD的一个法向量为

n2

=(x，y，z)，

PB

=(0，2，-2)，

BD

=(2，-2，0)，
由

n2 • PB =0 n2 • BD =0

得

2y-2z=0 2x-2y=0

取

n2

=(1，1，1)，
则cos＜

n1

，

n2

＞=

n1 • n2

| n1 |•| n2 |

=

-2

2 • 3

=-

6

3

，
故二面角C-PB-D的大小为arccos

6

3

．
（Ⅲ）存在满足条件的点M．
由（Ⅰ）可知，向量

PE

是平面PBC的一个法向量，
若在线段PE上存在一点M，使DM∥平面PBC，设

PM

=λ

PE

，
则

DM

=

DP

+

PM

=(-2，0，2)+λ(0，-1，-1)=(-2，-λ，2-λ)，由

DM

•

PE

=0，
得λ-（2-λ）=0，∴λ=1，即M点与线段PE的端点E重合．