题目内容
12．在三棱柱ABC-A1B1C1中，各棱长相等，侧棱垂直于底面，点D是侧面BB1C1C的中点，则AD与平面ABC所成角的大小是（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
分析 取BC的中点E，连接AE，DE，则DE⊥平面ABC，从而∠DAE为所求角，在Rt△ADE值计算tan∠DAE即可．
解答 
解：取BC的中点E，连接AE，DE，
则DE⊥底面ABC，∴∠DAE为AD与平面BC所成的角．
设三棱柱的棱长为1，则AE=$\frac{\sqrt{3}}{2}$，DE=$\frac{1}{2}$，
∴tan∠DAE=$\frac{DE}{AE}$=$\frac{\sqrt{3}}{3}$，
∴∠DAE=30°．
故选：A．
点评 本题考查了线面角的计算，作出所求的线面角是解题关键，属于基础题．
练习册系列答案
相关题目
2．在下列函数中，在定义域上是单调的奇函数的为（ ）
| A． | y=1 | B． | y=x-1 | C． | y=x+1 | D． | y=x3 |
20．设M={x|x=a2+1，a∈R}，P={y|y=b2-4b+5，b∈R}，则下列关系正确的是（ ）
| A． | M=P | B． | M?P | ||
| C． | P?M | D． | M与P没有公共元素 |
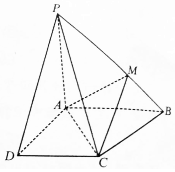如图，四棱锥P-ABCD中，PA⊥底面ABCD，∠BAD=∠ADC=$\frac{π}{2}$，AB=AD=AP=3，DC=2，点M在PB上，且PM=2MB．
1．在△ABC中，a=1，B=45°，面积S=2，则△ABC的外接圆的直径为（ ）
| A． | $6\sqrt{2}$ | B． | $4\sqrt{3}$ | C． | 5 | D． | $5\sqrt{2}$ |
如图O是等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高交于点G，且与AB，AC分别相切于E，F两点．