Question

【题目】已知正项等比数列是单调递增数列，且与的等差中项为，与的等比中项为16，.

（Ⅰ）求数列和的通项公式；

（Ⅱ）令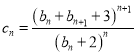，，求数列的前项和.

Answer 1

【答案】（Ⅰ）（Ⅱ）.

【解析】

（Ⅰ）设等比数列的公比为，由题意可知：，根据等比数列的通项公式、等差中项的公式、等比中项的公式，结合已知与的等差中项为，可以求出的值，再根据已知与的等比中项为16，可求出的值，写出的通项公式，最后根据对数运算性质求出数列的通项公式；

（Ⅱ）根据数列的通项公式，化简数列的通项公式，利用错位相减法、等比数列前项和公式，求出数列的前项和.

（Ⅰ）等比数列的公比为，由题意可知：，因为与的等差中项为，所以，

，又因为与的等比中项为16，所以而由题意可知，

.

（Ⅱ），

，记，

得：，

，所以数列的前项和

.