题目内容
(本小题满分14分)
如图①边长为1的正方形ABCD中,点E、F分别
为AB、BC的中点,将△BEF剪去,将
△AED、△DCF分别沿DE、DF折起,使A、
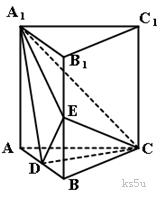
C两点重合于点P得一个三棱锥如图②示.
(1)求证: ;
;
(2)求三棱锥 的体积;
的体积;
(3)求DE与平面PDF所成角的正弦值.

如图①边长为1的正方形ABCD中,点E、F分别
为AB、BC的中点,将△BEF剪去,将
△AED、△DCF分别沿DE、DF折起,使A、
C两点重合于点P得一个三棱锥如图②示.
(1)求证:
 ;
;(2)求三棱锥
 的体积;
的体积; (3)求DE与平面PDF所成角的正弦值.


(1)证明:见解析;
(2)
 .
.
(3)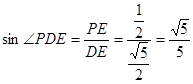
(2)

 .
.(3)
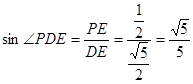
本试题主要考察了线面角的求解,以及垂体的体积的运用,和线线垂直的证明的综合运用。
(1)依题意知图①折前 ,∴
,∴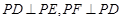 ,
,
∵ ∴
∴ 平面
平面 又∵
又∵ 平面
平面 ,利用线面垂直的性质定理得到结论。
,利用线面垂直的性质定理得到结论。
(2)三棱锥的体积可以利用转换顶点的思想来求解得到。
(3)根据由(2)知 又
又 ∴
∴ 平面
平面
∴ 为DE与平面PDF所成的角,然后借助于三角形得到求解。
为DE与平面PDF所成的角,然后借助于三角形得到求解。
(1)证明:依题意知图①折前 ,∴
,∴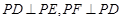 ,
,
∵ ∴
∴ 平面
平面 又∵
又∵ 平面
平面
∴
(2)解法1:依题意知图①中AE=CF= ∴PE= PF=
∴PE= PF= ,在△BEF中
,在△BEF中 ,
,
在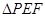 中,
中,
∴
∴
 .
.

【(2)解法2:依题意知图①中AE=CF= ∴PE= PF=
∴PE= PF= ,
,
在△BEF中 ,
,
取EF的中点M,连结PM
则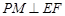 ,
, ∴
∴
∴
∴
 .
.
(3) 由(2)知 又
又 ∴
∴ 平面
平面
∴ 为DE与平面PDF所成的角,
为DE与平面PDF所成的角,
在 中,∵
中,∵ ,
,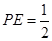
∴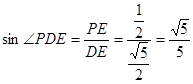
(1)依题意知图①折前
 ,∴
,∴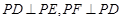 ,
,∵
 ∴
∴ 平面
平面 又∵
又∵ 平面
平面 ,利用线面垂直的性质定理得到结论。
,利用线面垂直的性质定理得到结论。(2)三棱锥的体积可以利用转换顶点的思想来求解得到。
(3)根据由(2)知
 又
又 ∴
∴ 平面
平面
∴
 为DE与平面PDF所成的角,然后借助于三角形得到求解。
为DE与平面PDF所成的角,然后借助于三角形得到求解。(1)证明:依题意知图①折前
 ,∴
,∴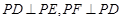 ,
,∵
 ∴
∴ 平面
平面 又∵
又∵ 平面
平面
∴

(2)解法1:依题意知图①中AE=CF=
 ∴PE= PF=
∴PE= PF= ,在△BEF中
,在△BEF中 ,
,在
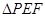 中,
中,
∴

∴

 .
.
【(2)解法2:依题意知图①中AE=CF=
 ∴PE= PF=
∴PE= PF= ,
,在△BEF中
 ,
,取EF的中点M,连结PM
则
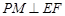 ,
, ∴
∴
∴

∴

 .
.(3) 由(2)知
 又
又 ∴
∴ 平面
平面
∴
 为DE与平面PDF所成的角,
为DE与平面PDF所成的角,在
 中,∵
中,∵ ,
,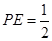
∴
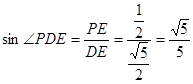

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 ,AP=
,AP= ,PC=
,PC= .
.
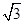 .
.
 ,则它们的体积之比是_______
,则它们的体积之比是_______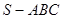 的所有棱长均为2,D是SA 的中点,E是BC 的中点,则
的所有棱长均为2,D是SA 的中点,E是BC 的中点,则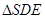 绕直线SE 转一周所得到的旋转体的表面积为 .
绕直线SE 转一周所得到的旋转体的表面积为 . ,侧面展开图的圆心角是
,侧面展开图的圆心角是 ,则圆锥的体积是_______.
,则圆锥的体积是_______. πr3;四维空间中“超球”的三维测度V=8πr3,则猜想其四维测度
πr3;四维空间中“超球”的三维测度V=8πr3,则猜想其四维测度 ▲ .
▲ .