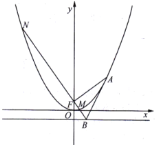
题目内容
【题目】抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,若
,若![]() 为抛物线上第一象限的一动点,过
为抛物线上第一象限的一动点,过![]() 作
作![]() 的垂线交准线
的垂线交准线![]() 于点
于点![]() ,交抛物线于
,交抛物线于![]() 两点.
两点.
(Ⅰ)求证:直线![]() 与抛物线相切;
与抛物线相切;
(Ⅱ)若点![]() 满足
满足![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
【答案】(I)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)设![]() ,由此可得直线
,由此可得直线![]() 的斜率,进而得到直线
的斜率,进而得到直线![]() 的斜率,由此得到
的斜率,由此得到![]() 的方程为
的方程为![]() ,令
,令![]() 可得点
可得点![]() 的坐标,于是可得直线
的坐标,于是可得直线![]() 的斜率.然后再由导数的几何意义得到在点A处的切线的斜率,比较后可得结论.(Ⅱ)由(Ⅰ)知
的斜率.然后再由导数的几何意义得到在点A处的切线的斜率,比较后可得结论.(Ⅱ)由(Ⅰ)知![]() ,直线
,直线![]() 的方程为
的方程为![]() ,将直线方程与椭圆方程联立消元后得到二次方程,结合根与系数的关系及
,将直线方程与椭圆方程联立消元后得到二次方程,结合根与系数的关系及![]() 可求得点A的坐标.
可求得点A的坐标.
(Ⅰ)由题意得焦点![]() .设
.设![]() ,
,
∴直线![]() 的斜率为
的斜率为![]() ,
,
由已知直线![]() 斜率存在,且直线
斜率存在,且直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴直线![]() 的斜率为
的斜率为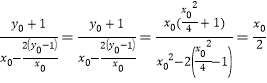 .
.
由![]() 得
得![]() ,
,
∴![]() ,即抛物线在点A处的切线的斜率为
,即抛物线在点A处的切线的斜率为![]() ,
,
∴直线![]() 与抛物线相切.
与抛物线相切.
(Ⅱ)由(Ⅰ)知![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由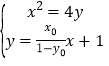 消去
消去![]() 整理得
整理得![]() ,
,
设![]() ,
,
则![]() .
.
由题意得直线![]() 的斜率为
的斜率为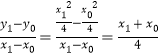 ,
,
直线![]() 的斜率为
的斜率为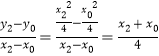 ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得![]() ,
,
解得![]() 或
或![]() .
.
∵![]() ,
,
∴![]() ,
,
又![]() ,且
,且![]() ,
,
∴存在![]() ,使得
,使得![]() .
.

练习册系列答案
相关题目