题目内容
已知点P（m，n）是位于第一象限，是在直线x+y-1=0上，则使不等式
恒成立的实数a的取值范围是 ________
（-∞，9]
分析：先根据点P的位置确定m，n的符号，再代入到直线x+y-1=0中得到m+n是定值，再求出
的最小值，最后令a小于等于该最小值即可．
解答：∵点P（m，n）是位于第一象限∴m＞0，n＞0
∴m+n-1=0即m+n=1
∵使不等式恒成立的实数a要满足a小于等于的最小值即可
∵
=1+4+
≥5+2
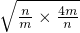=9
当且仅当n=2m，即n=
，m=
时等号成立
∴a≤9
故答案为：（-∞，9]．
点评：本题主要考查基本不等式的应用．基本不等式是高考的重点也是高考的热点问题，一定要做到灵活运用．
分析：先根据点P的位置确定m，n的符号，再代入到直线x+y-1=0中得到m+n是定值，再求出
的最小值，最后令a小于等于该最小值即可．解答：∵点P（m，n）是位于第一象限∴m＞0，n＞0
∴m+n-1=0即m+n=1
∵使不等式
恒成立的实数a要满足a小于等于的最小值即可∵
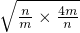=1+4+≥5+2=9当且仅当n=2m，即n=
，m=时等号成立∴a≤9
故答案为：（-∞，9]．
点评：本题主要考查基本不等式的应用．基本不等式是高考的重点也是高考的热点问题，一定要做到灵活运用．
练习册系列答案
相关题目
已知点P（m，n）是直线2x+y+5=0上的任意一点，则
的最小值为（ ）
| m2+n2 |
A、
| ||
B、
| ||
| C、5 | ||
| D、10 |