题目内容
设函数y=sin（2x+
），给出以下四个论断：
①它的图象关于直线x=
对称；
②它的图象关于点（
，0）对称；
③它的周期是π；
④在区间[-
，
]上是增函数．
正确的序号是 ．
| π |
| 3 |
①它的图象关于直线x=
| π |
| 12 |
②它的图象关于点（
| π |
| 3 |
③它的周期是π；
④在区间[-
| 5π |
| 12 |
| π |
| 12 |
正确的序号是
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：分别根据三角函数的周期性，对称性和单调性的性质进行判断即可得到结论．
解答：
解：在函数y=sin（2x+
）中，令2x+
=kπ+
，k∈z，
解得x=
+
，k∈z，
当k=0时，对称轴为x=
，
∴①正确．
②令2x+
=kπ，k∈z，解得 x=
-
，当k=1时，其对称中心为（
，0），k∈z，
∴②正确．
③函数的周期T=
=π，∴③正确．
④由-
+2kπ≤2x+
≤2kπ+
，
解得-
+kπ≤x≤kπ+
，k∈z，
当k=0时，函数的递增区间为[-
+kπ，kπ+
]，故④正确，
故答案为：①②③④
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
解得x=
| kπ |
| 2 |
| π |
| 2 |
当k=0时，对称轴为x=
| π |
| 12 |
∴①正确．
②令2x+
| π |
| 3 |
| kπ |
| 2 |
| π |
| 2 |
| π |
| 3 |
∴②正确．
③函数的周期T=
| 2π |
| 2 |
④由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得-
| 5π |
| 12 |
| π |
| 12 |
当k=0时，函数的递增区间为[-
| 5π |
| 12 |
| π |
| 12 |
故答案为：①②③④
点评：本题主要考查三角函数的图象和性质，要求熟练掌握相应的性质．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
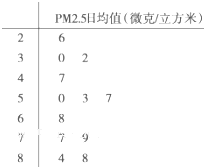PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75毫克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）：要得到函数y=2sin2x的图象，只需将y=sin2x-
cos2x的图象（ ）
| 3 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知数列{an }的前n项和为Sn，执行如图的程序框图，则输出的M一定满足（ ）
| A、Sn=nM | ||
B、Sn=
| ||
| C、Sn≤nM | ||
| D、Sn≥nM |