题目内容
11.已知函数$f(x)=\frac{1}{3}{x^3}+a{x^2}+(2a-1)x(a∈R)$.(Ⅰ)若f(x)在点(0,0)处的切线方程为y=x,求a的值;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)当a=-1时,设f(x)在x1,x2(x1<x2)处取到极值,记M(x1,f(x1)).A(0,f(0)),B(1,f(1)),C(2,f(2)),判断直线AM、BM、CM与函数f(x)的图象各有几个交点(只需写出结论).
分析 (Ⅰ)求出函数的导数,根据切线方程求出a的值即可;
(Ⅱ)通过讨论a的范围,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅲ)a=-1时,求出直线和f(x)的交点个数,写出结论即可.
解答 解:(Ⅰ)由题意f'(x)=x2+2ax+2a-1,…(1分)
因为f(x)在(0,0)点处切线方程为y=x,
所以f'(0)=2a-1=1,解得a=1,
经检验a=1时满足条件. …(3分)
(Ⅱ)由(I)f'(x)=x2+2ax+2a-1=(x+1)(x+2a-1)
令f'(x)=0,则x=-1或x=1-2a,…(4分)
①当a>1时,1-2a<-1,
令f'(x)>0,解得x<1-2a或x>-1;
令f'(x)<0,解得1-2a<x<-1.
所以函数f(x)的单调增区间为(-∞,1-2a)和(-1,+∞),
单调减区间为(1-2a,-1). …(6分)
②当a=1时,1-2a=-1,此时,f'(x)≥0恒成立,
且仅在x=-1处f'(x)=0,
故函数f(x)的单调增区间为(-∞,+∞).…(7分)
③当a<1时,1-2a>-1,
同理可得函数f(x)的单调增区间为(-∞,-1)和(1-2a,+∞),
单调减区间为(-1,1-2a).…(9分)
(Ⅲ)直线AM与f(x)的图象的交点个数是3个;…(10分)
直线BM与f(x)的图象的交点个数是3个;…(11分)
直线CM与f(x)的图象的交点个数是2个.…(13分)
点评 本题考查了切线方程问题,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
1.如图所示,程序框图的输出值S=( )


| A. | 21 | B. | 15 | C. | 28 | D. | -21 |
19.下列函数中既是奇函数又在区间(0,+∞)上单调递减的是( )
| A. | y=e-x | B. | y=ln(-x) | C. | y=x3 | D. | $y=\frac{1}{x}$ |
3.设$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,且$\overrightarrow{a}$≠±$\overrightarrow{b}$.则“|$\overrightarrow{a}$|=|$\overrightarrow{b}$|”是“($\overrightarrow{a}+\overrightarrow{b}$)⊥($\overrightarrow{a}-\overrightarrow{b}$)”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10. 如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )
如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )
 如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )
如图,⊙O与x轴的正半轴交点为A,点B,C在⊙O上,且B($\frac{4}{5}$,-$\frac{3}{5}$),点C在第一象限,∠AOC=α,BC=1,则cos($\frac{5π}{6}$-α)=( )| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
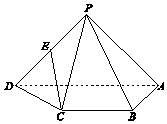 如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1
如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1