题目内容
18.在△ABC中,角A,B,C所对应的边分别为a,b,c,且(2a-c)cosB=bcosC.(Ⅰ)求角B的大小;
(Ⅱ)若a=2,c=3,求sinC的值.
分析 (Ⅰ)由正弦定理化简条件中的等式,利用两角和的正弦值求出cosB的值,从而求出B的大小;
(Ⅱ)根据余弦定理求出b的值,再由正弦定理求出sinC的值.
解答 解:(Ⅰ)△ABC中,(2a-c)cosB=bcosC,
由正弦定理得(2sinA-sinC)cosB=sinBcosC;
∴2sinAcosB=sinCcosB+sinBcosC=sin(B+C)=sinA.
∵0<A<π,
∴sinA≠0,
∴cosB=$\frac{1}{2}$,
又0<B<π,
∴B=$\frac{π}{3}$;
(Ⅱ)a=2,c=3,
由余弦定理得:b2=a2+c2-2accosB=22+32-2×2×3cos$\frac{π}{3}$=7,
∴b=$\sqrt{7}$;
再由正弦定理得
sinC=$\frac{csinB}{b}$=$\frac{3×sin\frac{π}{3}}{\sqrt{7}}$=$\frac{3\sqrt{21}}{14}$.
点评 本题考查了正弦、余弦定理的灵活应用问题,是综合题.

练习册系列答案
相关题目
9.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为x-ay=0,曲线C的一个焦点与抛物线y2=-8x的焦点重合,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{10}$ |
3.若$\overline z$是z的共轭复数,且满足$\overline z({1-i})$=3+i,则z=( )
| A. | 1+2i | B. | -1+2i | C. | 1-2i | D. | -1-2i |
7.执行如图所示的程序框图,如图输出S的值为-1,那么判断框内应填入的条件是( )
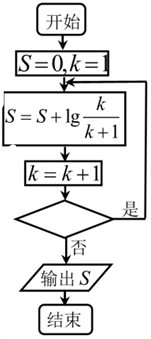

| A. | k≤8 | B. | k≤9 | C. | k≤10 | D. | k≤11 |
8.已知f(x)=$\left\{\begin{array}{l}{-2{x}^{2}+3x,-2≤x<0}\\{ln\frac{1}{x+1},0≤x≤2}\end{array}\right.$,若g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则实数a的取值范围为( )
| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | C. | (0,$\frac{1}{e}$) | D. | (0,$\frac{1}{2e}$) |