题目内容
抛物线
截直线
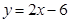所得的弦长等于
A． | B． | C． | D．15 |
D.
解析试题分析：由
得：
，设两交点A(
)B(
),则
，所以|AB|
。
考点：本题考查弦长公式。
点评：考查弦长公式的直接应用，我们应该熟练掌握弦长公式。属于基础题型。
练习册系列答案
同步练习强化拓展系列答案
相关题目
若直线
和⊙O:
没有交点,则过
的直线与椭圆
的交点个数 ( )
| A．至多一个 | B．0个 | C．1个 | D．2个 |
抛物线
的焦点到准线的距离是（ ）
A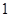． | B． | C． | D． |
若点
和点
分别为椭圆
的中心和左焦点，点
为椭圆上的任意一点， 则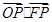
的最大值为（ ）
| A． | B． | C． | D． |
上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是（ ）
的焦点与椭圆
的一个焦点重合，过点
的直线与抛物线交于
两点，若
，则
的值（ ）
抛物线
（p＞0）上一点M到焦点的距离是a，则M到y轴的距离是（ ）
| A．a-p | B． a+p | C．a-  | D．a+2p |
已知P是以F1、F2为焦点的双曲线
上一点，若
，则三角形
的面积为（ ）
| A．16 | B． | C． | D． |
，过右焦点F作不垂直于
轴的弦交椭圆于A、B两点，AB的垂直平分线交
B．
C．
D．