题目内容
已知椭圆 ,过右焦点F作不垂直于
,过右焦点F作不垂直于 轴的弦交椭圆于A、B两点,AB的垂直平分线交
轴的弦交椭圆于A、B两点,AB的垂直平分线交 轴于N,则|NF|∶|AB|等于( )
轴于N,则|NF|∶|AB|等于( )
A. B.
B. C.
C. D.
D.
A
解析试题分析:根据已知条件,取直线的斜率为1.右焦点F(2,0).直线AB的方程为y=x-2.联立方程组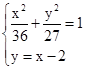 ,将y=x-2代入到椭圆中可知7x2-16x-92=0,设点设A(x1,y1),B(x2,y2),则x1+x2=
,将y=x-2代入到椭圆中可知7x2-16x-92=0,设点设A(x1,y1),B(x2,y2),则x1+x2=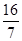 ,y1+y2=x1-2+x2-2=-
,y1+y2=x1-2+x2-2=-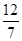 ,x1x2=-
,x1x2=-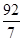 ,所以AB中点坐标为(
,所以AB中点坐标为(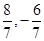 ),然后得到AB的垂直平分线方程,即为y+
),然后得到AB的垂直平分线方程,即为y+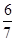 =-(x-
=-(x-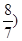 ,令y=0,得到x=
,令y=0,得到x=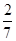 ,得到点N(
,得到点N(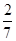 ,0),多以可知∴|NF|:|AB|=
,0),多以可知∴|NF|:|AB|=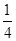 ,选A
,选A
考点:本试题主要考查了中心与椭圆的位置关系的运用,以及利用两点的距离公式表示线段的长的运用。
点评:特值法是求解选择题和填空题的有效方法.

练习册系列答案
相关题目
抛物线 截直线
截直线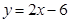 所得的弦长等于
所得的弦长等于
A. | B. | C. | D.15 |
已知点 在椭圆
在椭圆 上,则
上,则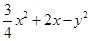 的最大值为( )
的最大值为( )
A. | B.-1 | C.2 | D.7 |
抛物线 的焦点到准线的距离为( )
的焦点到准线的距离为( )
| A.1 | B. | C. | D.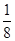 |
连接抛物线 的焦点
的焦点 与点
与点 所得的线段与抛物线交于点
所得的线段与抛物线交于点 ,设点
,设点 为坐标原点,则三角形
为坐标原点,则三角形 的面积为( )
的面积为( )
A. | B. | C. | D. |
设双曲线
 的一条渐近线与抛物线
的一条渐近线与抛物线 只有一个公共点,则双曲线的离心率为
只有一个公共点,则双曲线的离心率为
A. | B. | C. | D.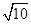 |
设椭圆 的右焦点与抛物线
的右焦点与抛物线 的焦点相同,离心率为
的焦点相同,离心率为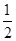 ,则此椭圆的方程为( )
,则此椭圆的方程为( )
A. | B. | C.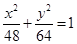 | D. |
在椭圆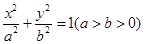 中,
中,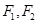 分别是其左右焦点,若
分别是其左右焦点,若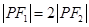 ,则该椭圆离心率的取值范围是
,则该椭圆离心率的取值范围是
A.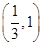 | B.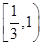 |
C.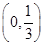 | D.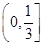 |
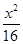 +
+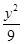 =1的两焦点,过点F2的直线交椭圆于A,B两点.在△AF1B中,若有两边之和是10,则第三边的长度为 ( )
=1的两焦点,过点F2的直线交椭圆于A,B两点.在△AF1B中,若有两边之和是10,则第三边的长度为 ( )