题目内容
已知a,b,c是三条不同的直线, 是三个不同的平面,上述命题中真命题的是
是三个不同的平面,上述命题中真命题的是
| A.若a⊥c,b⊥c,则a∥b或a⊥b |
B.若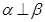 , ,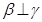 ,则 ,则 ∥ ∥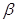 ; ; |
C.若a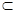  ,b ,b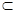 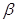 ,c ,c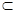 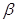 ,a⊥b, a⊥c,则 ,a⊥b, a⊥c,则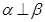 ; ; |
D.若a⊥ , b , b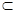 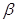 ,a∥b,则 ,a∥b,则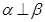 |
D
解析试题分析:若 ,则直线
,则直线 的位置关系可平行,可相交,可异面,故A错;若
的位置关系可平行,可相交,可异面,故A错;若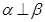 ,
,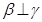 ,则
,则 ∥
∥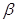 或
或 ,故B错;当直线
,故B错;当直线 时,
时, 不一定垂直,C错;因为
不一定垂直,C错;因为 且
且 ,故
,故 ,又
,又 ,所以
,所以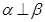 ,D正确.
,D正确.
考点:1、空间直线和直线的位置关系;2、平面和平面的位置关系;3、面面垂直的判定.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 , ,   则 则 |
B.若 ,则 ,则 |
C.若 , ,  则 则 |
D.若   则 则 |
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )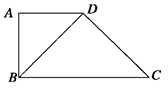
| A.平面ABD⊥平面ABC | B.平面ADC⊥平面BDC |
| C.平面ABC⊥平面BDC | D.平面ADC⊥平面ABC |
如图所示,直线 垂直于⊙
垂直于⊙ 所在的平面,
所在的平面, 内接于⊙
内接于⊙ ,且
,且 为⊙
为⊙ 的直径,点
的直径,点 为线段
为线段 的中点.现有结论:①
的中点.现有结论:① ;②
;② 平面
平面 ;③点
;③点 到平面
到平面 的距离等于线段
的距离等于线段 的长.其中正确的是( )
的长.其中正确的是( )
| A.①② | B.①②③ | C.① | D.②③ |
已知 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
| A.AC⊥SB |
| B.AB∥平面SCD |
| C.AB与SC所成的角等于DC与SA所成的角 |
| D.SA与平面SBD所成的角等于SC与平面SBD所成的角 |
正方体 的棱长为
的棱长为 ,线段
,线段 上有两个动点
上有两个动点 ,且
,且 ,
,
则下列结论中错误的是( )
A. |
B.三棱锥 的体积为定值 的体积为定值 |
C.二面角 的大小为定值 的大小为定值 |
D.异面直线 所成角为定值 所成角为定值 |
过直线 外两点作与直线
外两点作与直线 平行的平面,可以作( )
平行的平面,可以作( )
| A.1个 | B.1个或无数个 |
| C.0个或无数个 | D.0个、1个或无数个 |
已知 为两条不同的直线,
为两条不同的直线, 为两个不同的平面,给出下列4个命题:
为两个不同的平面,给出下列4个命题:
①若 ②若
②若
③若 ④若
④若
其中真命题的序号为( )
| A.①② | B.②③ | C.③④ | D.①④ |