题目内容
设x,y为实数,满足3≤xy2≤8,4≤
≤9,则
的最大值是
| x2 |
| y |
| x2 |
| y4 |
9
9
.分析:先用待定系数法,可得
=(xy2)-
(
)
,再利用不等式的性质,求得4
≤ (
)
≤9
,8-
≤(xy2)-
≤3-
两式相乘,即可得到结论.
| x2 |
| y4 |
| 6 |
| 5 |
| x2 |
| y |
| 8 |
| 5 |
| 8 |
| 5 |
| x2 |
| y |
| 8 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
解答:解:设
=(xy2)m(
)n,∴
,∴
∴
=(xy2)-
(
)
∵4≤
≤9,∴4
≤ (
)
≤9
①.
又∵3≤xy2≤8,∴8-
≤(xy2)-
≤3-
②,
①×②可得:4
×8-
≤ (xy2)-
(
)
≤9
×3-
.
∴2-
≤
≤ 9,当且仅当
=9,且xy2=3,
即x=3,y=1时,
的最大值是9.
故答案为:9.
| x2 |
| y4 |
| x2 |
| y |
|
|
∴
| x2 |
| y4 |
| 6 |
| 5 |
| x2 |
| y |
| 8 |
| 5 |
∵4≤
| x2 |
| y |
| 8 |
| 5 |
| x2 |
| y |
| 8 |
| 5 |
| 8 |
| 5 |
又∵3≤xy2≤8,∴8-
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
①×②可得:4
| 8 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| x2 |
| y |
| 8 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |
∴2-
| 2 |
| 5 |
| x2 |
| y4 |
| x2 |
| y |
即x=3,y=1时,
| x2 |
| y4 |
故答案为:9.
点评:本题考查不等式的性质,考查求最大值,解题的关键是正确运用不等式的性质.

练习册系列答案
相关题目
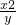 ≤9,则
≤9,则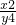 的最大值是________.
的最大值是________.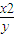 ≤9,则
≤9,则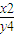 的最大值是 .
的最大值是 .