题目内容

19．如图为一个几何体的三视图，则该几何体外接球的表面积为（　　）
A．4$\sqrt{3}$πB．12πC．12$\sqrt{3}$πD．24π

分析 几何体为直三棱柱，作出直观图，根据三棱柱的结构特征找出外接球的球心外置，计算半径．

解答 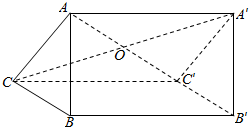解：由三视图可知该几何体为直三棱柱ABC-A'B'C'，
作出直观图如图所示：则AB⊥BC，AB=BC=2，AA'=2．∴AC=2$\sqrt{2}$．
∴三棱柱的外接球球心为平面ACC'A'的中心O，
∴外接球半径r=OA=$\frac{1}{2}$AC'=$\frac{1}{2}$$\sqrt{{2}^{2}+（2\sqrt{2}）^{2}}$=$\sqrt{3}$．
∴外接球的表面积S=4π×$（\sqrt{3}）^{2}$=12π．
故选B．

点评 本题考查了棱柱与外接球的三视图和结构特征，属于中档题．

练习册系列答案
相关题目
9．已知虚数$z=\frac{5}{3-4i}-\frac{4+3i}{5}$，则z的虚部是（　　）
A．$-\frac{1}{5}$B．$-\frac{1}{5}i$C．$\frac{1}{5}$D．$\frac{1}{5}i$
10．已知椭圆$\frac{{x}^{2}}{{b}^{2}}$+$\frac{{y}^{2}}{{a}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且a2=2b．
（1）求椭圆的方程；
（2）直线l：x-y+m=0与椭圆交于A，B两点，是否存在实数m，使线段AB的中点在圆x2+y2=5上，若存在，求出m的值；若不存在，说明理由．
7．函数f（x）=2sin（ωx+φ）的部分图象如图所示，则ω，φ的值分别是（　　）
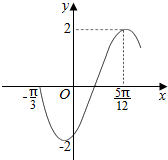
A．2，-$\frac{π}{3}$B．2，-$\frac{π}{6}$C．4，-$\frac{π}{6}$D．4，$\frac{π}{3}$
14．直线l：$\frac{x}{4}+\frac{y}{3}=1$与x轴、y轴分别相交于点A、B，O为坐标原点，则△OAB的内切圆的方程为（x-1）2+（y-1）2=1．
4．已知4sinα+3cosα=0，则$\frac{{sin（{4π-α}）cos（{5π+α}）cos（{\frac{9π}{2}+α}）cos（{\frac{15π}{2}-α}）}}{{cos（{π-α}）sin（{3π-α}）sin（{9π-α}）sin（{\frac{13π}{2}+α}）}}$=$\frac{3}{4}$．
11．已知数列{an}的前n项和Sn=an+$\frac{1}{2}{n^2}+\frac{3}{2}n-2（n∈{N^*}）$．
（1）求数列{an}的通项公式；
（2）若bn=$\left\{\begin{array}{l}\frac{1}{{（{a_n}-1）（{a_n}+1）}}，n为奇数\\ 4（\frac{1}{2}{）^{a_n}}，n为偶数\end{array}$，且数列{bn}的前n项和为Tn，求T2n．
8．已知曲线f（x）=ex-ax在点（0，f（0））处的切线方程为3x+y+b=0，则下列不等式恒成立的是（　　）
A．f（x）≥2-4ln2B．f（x）≤2-4ln2C．f（x）≥4-8ln2D．f（x）≤4-8ln2
9．已知△ABC中，a，b，c分别为内角A，B，C的对边，且a•cosB+b•cosA=3c•cosC，则cosC=$\frac{1}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网