题目内容
已知偶函数y=f(x)满足:当x≥2时,f(x)=(x-2)(a-x),a∈R,当x∈[0,2)时,f(x)=x(2-x)
(Ⅰ)求f(x)表达式;
(Ⅱ)若直线y=1与函数y=f(x)的图象恰有两个公共点,求实数a的取值范围;
(Ⅲ)试讨论当实数a、m满足什么条件时,直线y=m和函数y=f(x)的图象恰有k个公共点(k≥3),
且这k个公共点均匀分布在直线y=m上.(不要求过程)
(Ⅰ)求f(x)表达式;
(Ⅱ)若直线y=1与函数y=f(x)的图象恰有两个公共点,求实数a的取值范围;
(Ⅲ)试讨论当实数a、m满足什么条件时,直线y=m和函数y=f(x)的图象恰有k个公共点(k≥3),
且这k个公共点均匀分布在直线y=m上.(不要求过程)
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(Ⅰ)先设x≤-2,则-x≥2,再设,设x∈(-2,0),则-x∈[0,2),再利用函数是偶函数可求;
(Ⅱ)分a>2与a≤2进行讨论可求;
(Ⅲ)结合函数的图象进行讨论,综合可得答案.
(Ⅱ)分a>2与a≤2进行讨论可求;
(Ⅲ)结合函数的图象进行讨论,综合可得答案.
解答:
(Ⅰ).设x≤-2,则-x≥2,
∴f(-x)=(-x-2)(a+x)
又∵f(x)偶函数
∴f(x)=f(-x)
∴f(x)=(x+a)(-x-2)=-(x+2)(x+a),
设x∈(-2,0),则-x∈[0,2),
∴f(-x)=x(2+x)=f(x),
故f(x)=
(Ⅱ)①a>2时x≥2,f(x)=(x-2)(a-x),
f(x)max=f(1+
)=(
-1)2,
∴(
-1)2<1,
∴0<a<4,
∴2<a<4
②a≤2时,都满足综上,
所以 a∈(-∞,4);
(Ⅲ).当a≤2时,m=
或m=0;
当2<a<2+
时,m=
;此时f(
)<
当a=4时,m=0,m=
或m=1;
当a>
时,m=
.此时m=f(
)>1.
∴f(-x)=(-x-2)(a+x)
又∵f(x)偶函数
∴f(x)=f(-x)
∴f(x)=(x+a)(-x-2)=-(x+2)(x+a),
设x∈(-2,0),则-x∈[0,2),
∴f(-x)=x(2+x)=f(x),
故f(x)=
|
(Ⅱ)①a>2时x≥2,f(x)=(x-2)(a-x),
f(x)max=f(1+
| a |
| 2 |
| a |
| 2 |
∴(
| a |
| 2 |
∴0<a<4,
∴2<a<4
②a≤2时,都满足综上,
所以 a∈(-∞,4);
(Ⅲ).当a≤2时,m=
| 3 |
| 4 |
当2<a<2+
| 3 |
| 3 |
| 4 |
| 2+a |
| 2 |
| 3 |
| 4 |
当a=4时,m=0,m=
| 3 |
| 4 |
当a>
10+
| ||
| 3 |
| 3a2-20a+12 |
| 16 |
| 2+a |
| 4 |
点评:本题考查函数的性质,解析式的求解及分类讨论的数学思想,属于难题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
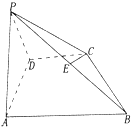 如图在四锥P-ABCD中,CD⊥平面PAD,CD∥AB,AB=2CD,PD=AD,E为PB中点.证明:
如图在四锥P-ABCD中,CD⊥平面PAD,CD∥AB,AB=2CD,PD=AD,E为PB中点.证明: