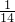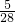Question

已知袋中装有3个红球与6个黄球，这些小球的外形与重量都相同，现需要一个黄球使用，某人每次从中任取一个并不放回，则他直到第3次才取得黄球的概率为（　　）

• A．

  1

  14

• B．

  2

  3

• C．

  2

  27

• D．

  5

  28

Answer 1

分析：有9只小球，第一次从中取一只红色的概率是

1

3

，第二次从中取一只红色的概率

3

8

，第三次从中取一只黄色的概率是

6

7

，每次取得什么灯泡相互之间没有影响，由相互独立事件的概率公式得到结果．

解答：解：∵盒中装有3个红球与6只黄色小球
第一次从中取一只红色的概率是

1

3

，第二次从中取一只红色的概率

1

4

，第三次从中取一只黄色的概率是

6

7

，每次取得什么灯泡相互之间没有影响
由相互独立事件的概率公式得P=

1

3

×

2

8

×

6

7

=

1

14

，
故选A

点评：本题主要考查了相互独立事件概率公式的应用，解题中要注意不放回抽取事件对概率的影响．