题目内容
12.若${({x^2}+\frac{1}{{2\sqrt{x}}})^n}$(n∈N*)的二项展开式中第3项和第5项的二项式系数相等,则展开式中系数最大的项的系数为$\frac{15}{4}$.分析 根据在${({x^2}+\frac{1}{{2\sqrt{x}}})^n}$(n∈N*)的展开式中第3项与第5项的二项式系数相等,得到${C}_{n}^{2}$=${C}_{n}^{4}$,解得n=6,写出二项式的通项公式,设二项式(x2+$\frac{1}{2\sqrt{x}}$)6的展开式的系数最大的项为第r+1项,所以$\left\{\begin{array}{l}{{T}_{r+1}≥{T}_{r}}\\{{T}_{r+1}≥{T}_{r+2}}\end{array}\right.$,解不等式即可得到所求系数.
解答 解:若${({x^2}+\frac{1}{{2\sqrt{x}}})^n}$(n∈N*)的二项展开式中第3项和第5项的二项式系数相等,
则${C}_{n}^{2}$=${C}_{n}^{4}$,解得n=6,
二项式(x2+$\frac{1}{2\sqrt{x}}$)6的展开式通项公式为Tr+1=${C}_{6}^{r}$(x2)6-r($\frac{1}{2\sqrt{x}}$)r=${C}_{6}^{r}$($\frac{1}{2}$)rx${\;}^{12-\frac{5r}{2}}$,
设二项式(x2+$\frac{1}{2\sqrt{x}}$)6的展开式的系数最大的项为第r+1项,
所以$\left\{\begin{array}{l}{{T}_{r+1}≥{T}_{r}}\\{{T}_{r+1}≥{T}_{r+2}}\end{array}\right.$,
即$\left\{\begin{array}{l}{{C}_{6}^{r}(\frac{1}{2})^{r}{≥C}_{6}^{r-1}(\frac{1}{2})^{r-1}}\\{{C}_{6}^{r}(\frac{1}{2})^{r}{≥C}_{6}^{r+1}(\frac{1}{2})^{r+1}}\end{array}\right.$,
解得$\frac{4}{3}$≤r≤$\frac{7}{3}$,r为正整数
所以r=2,
则展开式中系数最大的项为第3项,即系数为${C}_{6}^{2}$($\frac{1}{2}$)2=$\frac{15}{4}$.
故答案为:$\frac{15}{4}$.
点评 本题考查二项式系数的性质,本题解题的关键是正确利用二项式系数的性质,注意和组合数联系,本题是中档题.

| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 320 | 30 | 80 | 40 | 30 |
(Ⅱ)画出频率分布直方图;
(Ⅲ)求灯泡寿命在100h~400h的频率.

| A. | i>20 | B. | i<20 | C. | i>=20 | D. | i<=20 |
 如图,在平行六面体ABCD-A1B1C1D1中,已知$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,$\overrightarrow{A{A_1}}=\overrightarrow c$,则用向量$\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$可表示向量$\overrightarrow{B{D_1}}$等于( )
如图,在平行六面体ABCD-A1B1C1D1中,已知$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,$\overrightarrow{A{A_1}}=\overrightarrow c$,则用向量$\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$可表示向量$\overrightarrow{B{D_1}}$等于( )| A. | $\overrightarrow a+\overrightarrow b+\overrightarrow c$ | B. | $\overrightarrow a-\overrightarrow b+\overrightarrow c$ | C. | $\overrightarrow a+\overrightarrow b-\overrightarrow c$ | D. | $-\overrightarrow a+\overrightarrow b+\overrightarrow c$ |
| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
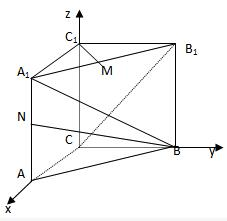 如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.