题目内容
数列{an}满足an+1=
，若a1=
，则a17=（ ）
|
| 6 |
| 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：数列递推式
专题：计算题,点列、递归数列与数学归纳法
分析：利用数列{an}满足an+1=
，a1=
，计算前几项，可得数列{an}是以3为周期的周期数列，即可求出a17．
|
| 6 |
| 7 |
解答：
解：∵数列{an}满足an+1=
，a1=
，
∴a2=
，a3=
，a4=
，
∴数列{an}是以3为周期的周期数列，
∵17=3×5+2，
∴a17=a2=
，
故选：B．
|
| 6 |
| 7 |
∴a2=
| 5 |
| 7 |
| 3 |
| 7 |
| 6 |
| 7 |
∴数列{an}是以3为周期的周期数列，
∵17=3×5+2，
∴a17=a2=
| 5 |
| 7 |
故选：B．
点评：本题考查数列递推式，考查学生的计算能力，确定数列{an}是以3为周期的周期数列是关键．
练习册系列答案
相关题目
正四面体ABCD的棱长为1，其中线段AB∥平面α，E，F分别是线段AD和BC的中点，当正四面体绕以AB为轴旋转时，线段EF在平面α上的射影E1F1长的范围是（ ）
A、[0，
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
执行如图所示的程序框图，则输出的a为（ ）
| A、20 | B、14 | C、10 | D、7 |
已知命题p：lnx＞0，命题q：ex＞1，则命题p是命题q（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
给出下列等式
①
=
②
=a
③{y|y=-x2+x-1，x≥1}∩{x|x=
-2，m≥0}={-1}
④{x||1-2x|＜5}∪{x|6-x-x2＞0}={x|-
＞0}
则上述等式成立的是（ ）
①
log51-log5
|
| 1-2log52 |
②
| a6 | ||||
|
| 6 |
| 5 |
③{y|y=-x2+x-1，x≥1}∩{x|x=
| m+1 |
④{x||1-2x|＜5}∪{x|6-x-x2＞0}={x|-
| x+3 |
| x-3 |
则上述等式成立的是（ ）
| A、①③ | B、①② | C、①④ | D、①③④ |
若向量
=（1，2），
=（4，5），则
=（ ）
| BA |
| CA |
| BC |
| A、（5，7） |
| B、（-3，-3） |
| C、（3，3） |
| D、（-5，-7） |
若
=（x，3），
=（3，1）且
∥
，则x的值是（ ）
| a |
| b |
| a |
| b |
| A、-9 | B、-1 | C、1 | D、9 |
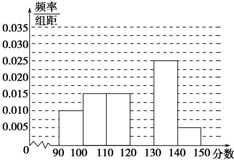某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六组[90，100），[100，110），…，[140，150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：