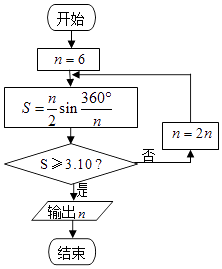
题目内容
【题目】已知曲线 ![]() 在
在 ![]() 的上方,且曲线
的上方,且曲线 ![]() 上的任意一点到点
上的任意一点到点 ![]() 的距离比到直线
的距离比到直线 ![]() 的距离都小1.
的距离都小1.
(Ⅰ)求曲线 ![]() 的方程;
的方程;
(Ⅱ)设 ![]() ,过点
,过点 ![]() 的直线与曲线
的直线与曲线 ![]() 相交于
相交于 ![]() 两点.
两点.
①若 ![]() 是等边三角形,求实数
是等边三角形,求实数 ![]() 的值;
的值;
②若 ![]() ,求实数
,求实数 ![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)设点 ![]() 曲线
曲线 ![]() 上任意一点,由题设有
上任意一点,由题设有 ![]() ,
,
于是 ![]() ,整理得
,整理得 ![]() .
.
由于曲线 ![]() 在
在 ![]() 轴的上方,所以
轴的上方,所以 ![]() .
.
所以曲线 ![]() 的方程为
的方程为 ![]() .
.
(Ⅱ)设 ![]() .
.
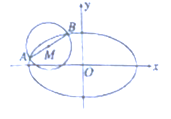
由题意 ![]() ,即
,即 ![]() ,
,
于是 ![]() ,
,
将 ![]() 代入,得
代入,得 ![]() ,由
,由 ![]() ,得
,得 ![]() .
.
从而 x1=-x2,
所以 ![]() .
.
因为 ![]() 是等边三角形,所以
是等边三角形,所以 ![]() .
.
将 ![]() 代入,
代入, ![]() ,解得
,解得 ![]() ,此时
,此时 ![]() .
.
设直线 ![]() ,
,
联立 ![]() 得
得 ![]() ,
, ![]() ,
,
![]() .
.
![]() ,
, ![]()
于是 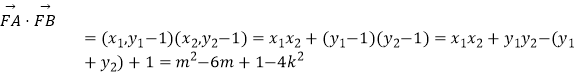
因为 ![]() ,即
,即 ![]() .
.
因 ![]() ,从而
,从而 ![]() .
.
解得 ![]() ..
..
【解析】(1)根据题意设出点P的坐标由抛物线的定义可得出等式求出曲线的方程即可。(2)由已知分别设出A、B两点的坐标利用已知 | A F | = | B F | ,把两点分别代入到抛物线的方程整理即到x1=-x2,借助三角形是等边三角形求出m的值,然后设出直线的方程联立直线与抛物线的方程由韦达定理分别求出x1+x2、x1x2关于m的代数式,进而可用坐标表示出![]() ,令其小于零解出m的取值范围即可。
,令其小于零解出m的取值范围即可。

练习册系列答案
相关题目