题目内容
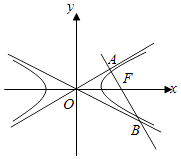
【题目】如图：已知抛物线 C1：y2=2px （p＞0），直线 l 与抛物线 C 相交于 A、B 两点，且当倾斜角为 60°的直线 l 经过抛物线 C1 的焦点 F 时，有|AB|= 
．
（Ⅰ）求抛物线 C 的方程；
（Ⅱ）已知圆 C2：（x﹣1）2+y2= 
，是否存在倾斜角不为 90°的直线 l，使得线段 AB 被圆 C2 截成三等分？若存在，求出直线 l 的方程；若不存在，请说明理由．
【答案】【解答】（I）当直线l的倾斜角为60°时，直线l的方程为y= 
（x﹣ 
），
联立方程组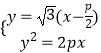 
，消元得3x2﹣5px+ 
=0，
∴|AB|= 
+p= 
，解得p= 
，
∴抛物线C的方程为y2= 
．
（II）假设存在直线l，使得AB被圆C2三等分，设直线l与圆C2的交点为C，D，
设直线l的方程为x=my+b，A（x1，y1），B（x2，y2），
联立方程组 
，得4y2﹣my﹣b=0，
∴y1+y2= 
，y1y2=﹣ 
，∴x1+x2=m（y1+y2）+2b= 
+2b，
∴AB的中点坐标为M（ 
+b， 
），
又圆C2的圆心为C2（1，0），∴k 
= 
，
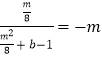即m2+8b﹣7=0，∴b= 
．
又|AB|= 
= 
．
∵圆心C2（1，0）到直线l的距离d= 
，圆C2的半径为 
，
∴|CD|=2 
= 
，
又|AB|= = ．C，D为AB的三等分点，
∴|AB|=3|CD|，
∴ = 
，解得m=± 
，∴b= 
．
∴直线l的方程为y=± x+ ．
【解析】（I）联立方程组，利用根与系数的关系和抛物线的性质列方程解出p；
（II）设直线l的方程为x=my+b，与抛物线方程联立，求出AB的中点坐标，利用垂径定理列方程求出m，b的关系。利用弦长公式计算求出|AB|，|CD|，根据|AB|=3|CD|解得m的值和直线l的方程。
