题目内容
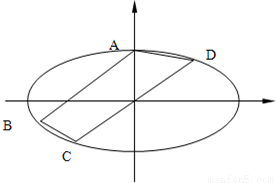
已知椭圆G：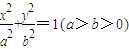
过点A（0，5），B（-8，3），直线CD过坐标原点O，且在线段AB的右下侧，求：（1）椭圆G的方程；
（2）四边形ABCD的面积的最大值．
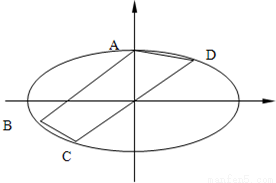
【答案】分析：（1）先将点A（0，5），B（-8，3），代入椭圆的方程解得：a=10 b=5，最后写出椭圆G的方程；
（2）连OB，则四边形ABCD的面积=S△OAD+S△OAB+S△OBC，=
|yB|AO+
dA×OD+
dB×OC，dA，dB分别表示A，B到直线CD的距离，设CD：-kx+y=0，代入椭圆方程消去y得到关于x的一元二次方程，再结合求根公式即可求得四边形ABCD的面积，最后结合基本不等式求最大值，从而解决问题．
解答：解：（1）将点A（0，5），B（-8，3），代入椭圆的方程得：b=5，且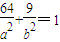
解得：a=10 b=5，椭圆G的方程为：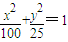
（2）连OB，则四边形ABCD的面积：S△OAD+S△OAB+S△OBC=
|yB|AO+
dA×OD+
dB×OC
dA，dB分别表示A，B到直线CD的距离，设CD：-kx+y=0，代入椭圆方程得：
x2+4k2x2-100=0，
∴D（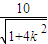
，
）
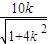OC=OD=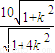
，
又yA=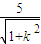
，yB=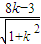
，
∴四边形ABCD的面积：S△OAD+S△OAB+S△OBC=
|yB|×AO+
dA×OD+
dB×OC
=
+
×
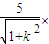
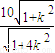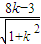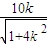=20+10×
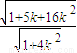≤20+10
．
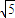四边形ABCD的面积的最大值为：20+10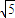
．
点评：本小题主要考查椭圆的标准方程、椭圆的简单性质、基本不等式等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．
（2）连OB，则四边形ABCD的面积=S△OAD+S△OAB+S△OBC，=
|yB|AO+dA×OD+dB×OC，dA，dB分别表示A，B到直线CD的距离，设CD：-kx+y=0，代入椭圆方程消去y得到关于x的一元二次方程，再结合求根公式即可求得四边形ABCD的面积，最后结合基本不等式求最大值，从而解决问题．解答：解：（1）将点A（0，5），B（-8，3），代入椭圆的方程得：b=5，且
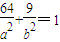
解得：a=10 b=5，椭圆G的方程为：
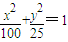
（2）连OB，则四边形ABCD的面积：S△OAD+S△OAB+S△OBC=
|yB|AO+dA×OD+dB×OCdA，dB分别表示A，B到直线CD的距离，设CD：-kx+y=0，代入椭圆方程得：
x2+4k2x2-100=0，
∴D（
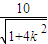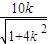，）OC=OD=
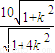，又yA=
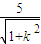，yB=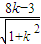，∴四边形ABCD的面积：S△OAD+S△OAB+S△OBC=
|yB|×AO+dA×OD+dB×OC=
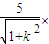
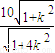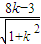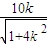+×=20+10×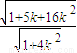≤20+10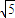．四边形ABCD的面积的最大值为：20+10
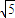．点评：本小题主要考查椭圆的标准方程、椭圆的简单性质、基本不等式等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
过点(m，0)，作圆x2＋y2＝1的切线l，交椭圆G于A，B两点．
，点A、B分别是椭圆C的左顶点和上顶点，直线AB与圆G： 
（
是椭圆的焦半距）相离，P是直线AB上一动点，过点P作圆G的两切线，切点分别为M、N．
、
，求椭圆C的方程；
的值（O是坐标原点）；
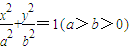，点A、B分别是椭圆C的左顶点和上顶点，直线AB与圆G：
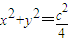（c是椭圆的焦半距）相离，P是直线AB上一动点，过点P作圆G的两切线，切点分别为M、N．
、
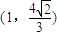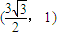，求椭圆C的方程；
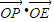的值（O是坐标原点）；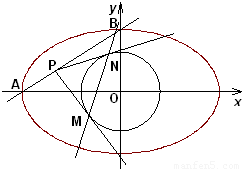
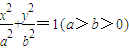过点A（0，5），B（-8，3），直线CD过坐标原点O，且在线段AB的右下侧，求：