题目内容
(本小题15分)
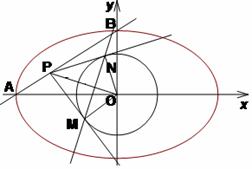
已知椭圆C:![]() ,点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:
,点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G: ![]() (
(![]() 是椭圆的焦半距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
是椭圆的焦半距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(1)若椭圆C经过两点![]() 、
、![]() ,求椭圆C的方程;
,求椭圆C的方程;
(2)当![]() 为定值时,求证:直线MN经过一定点E,并求
为定值时,求证:直线MN经过一定点E,并求![]() 的值(O是坐标原点);
的值(O是坐标原点);
(3)若存在点P使得△PMN为正三角形,试求椭圆离心率的取值范围.

解:(1)令椭圆![]() ,其中
,其中![]() ,
,
得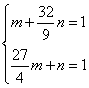 ,所以
,所以![]() ,即椭圆为
,即椭圆为![]() . ………3分
. ………3分
(2)直线![]() ,
,
设点![]() ,则
,则![]() 中点为
中点为![]() ,
,
所以点![]() 所在的圆的方程为
所在的圆的方程为![]() ,
,
化简为![]() , ………5分
, ………5分
与圆![]() 作差,即有直线
作差,即有直线![]() ,
,
因为点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,
,
所以![]() ,所以
,所以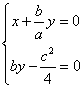 ,
,
 得
得![]() ,故定点
,故定点![]() , …8分
, …8分
![]() . ………9分
. ………9分
(3)由直线AB与圆G: ![]() (
(![]() 是椭圆的焦半距)相离,
是椭圆的焦半距)相离,
则![]() ,即
,即![]() ,
,![]() ,
,
得![]()
因为![]() , 所以
, 所以![]() ,① ………11分
,① ………11分
连接![]() 若存在点
若存在点![]() 使
使![]() 为正三角形,则在
为正三角形,则在![]() 中,
中,![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,得
,得![]()
因为![]() ,所以
,所以![]() ,② ………14分
,② ………14分
由①②,![]() ,
,
所以![]() . ………15分
. ………15分

练习册系列答案
相关题目
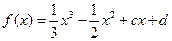 有极值.
有极值.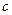 的取值范围;
的取值范围;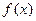 在
在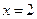 处取得极值,且当
处取得极值,且当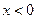 时,
时,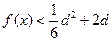 恒成立,求
恒成立,求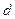 的取值范围.
的取值范围. 在一个周期内的图象如下图所示.
在一个周期内的图象如下图所示.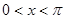 ,且方程
,且方程 有两个
有两个

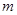 的取值范围.
的取值范围.
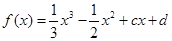 有极值.
有极值.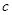 的取值范围;
的取值范围;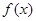 在
在 处取得极值,且当
处取得极值,且当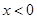 时,
时,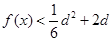 恒成立,求
恒成立,求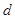 的取值范围.
的取值范围.