题目内容
如图,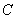 是以
是以 为直径的圆
为直径的圆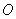 上异于
上异于 的点,平面
的点,平面 平面
平面 ,
, ,
, ,
, 分别是
分别是 的中点,记平面
的中点,记平面 与平面
与平面 的交线为
的交线为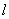 .
.
(1)求证:直线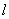
 平面
平面 ;
;
(2)直线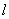 上是否存在点
上是否存在点 ,使直线
,使直线 分别与平面
分别与平面 、
、
直线 所成的角互余?若存在,求出
所成的角互余?若存在,求出 的值;若不存 在,请说明理由.
的值;若不存 在,请说明理由.

(1)证明: 分别为
分别为 中点,
中点, ,又
,又
 //平面EFA
//平面EFA
又BC 平面ABC,平面EFA∩平面ABC=
平面ABC,平面EFA∩平面ABC=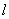

又BC⊥AC,平面PAC∩平面ABC=AC,平面PAC⊥平面ABC
∴BC⊥平面PAC ∴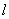 ⊥平面PAC
⊥平面PAC
(2)以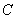 为坐标原点,
为坐标原点, 所在的直线为
所在的直线为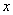 轴,
轴, 所在的直线为
所在的直线为 轴,过
轴,过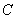 垂直面
垂直面 的
的
直线为 轴建立空间直角坐标系
轴建立空间直角坐标系
则
 ,
, 设
设 ,平面
,平面 的法向量为
的法向量为
则 即
即
令 得到平面
得到平面 的一个法向量为
的一个法向量为
 <
< >|
>|
 ,|
,| <
< ,
, >|=
>|=
依题意得 =
=



练习册系列答案
相关题目
图中的三角形称为希尔宾斯三角形,在下列四个三角形中,黑
色三角形的个数依次构成数列 的前四项,依此着色方案继
的前四项,依此着色方案继
续对三角形着色.

(1)数列 的通项公式
的通项公式 _____________;
_____________;
|
 满足
满足 ,记
,记 ,则
,则 的个位数字是_________.
的个位数字是_________.  的值为________.
的值为________. 相交于
相交于 、
、 两点,线段
两点,线段 ,直线
,直线 的斜率为
的斜率为 ,则
,则
 B.
B. C.
C. D.
D.
 =(3,4),
=(3,4), =(2,-1),如果向量
=(2,-1),如果向量 与
与 垂直,则x的值为( )
垂直,则x的值为( ) B.
B. C.
C.  D.2
D.2 B.
B.  C.
C.  D.
D.


 ,
, ,则
,则 是
是 成立的 ( )
成立的 ( )