��Ŀ����
��ԲC��![]() �����ҽ���ֱ���F1��F2��������Ϊ
�����ҽ���ֱ���F1��F2��������Ϊ![]() ��F���Ҵ�ֱ��x���ֱ�߱���ԲC�صõ��߶γ�Ϊl��
��F���Ҵ�ֱ��x���ֱ�߱���ԲC�صõ��߶γ�Ϊl��
(��)����ԲC�ķ��̣�
(��)��P����ԲC�ϳ�����˵������һ�㣬����PF1��PF2�����F1PF2�Ľ�ƽ����PM��C�ij����ڵ�M(m��0)����m��ȡֵ��Χ��
(��)��(��)�������£�����p��б��Ϊk��ֱ��l��ʹ��l����ԲC����ֻ��һ�������㣮
��ֱ��PF1��PF2��б�ʷֱ�Ϊk1��k2����k��0����֤��![]() Ϊ��ֵ������������ֵ��
Ϊ��ֵ������������ֵ��
�𰸣�
������
������
|
����(1) ����(2) ����(3)�� |

��ϰ��ϵ�д�
�����Ŀ
 ��2013•���ʶ�ģ��
��2013•���ʶ�ģ�� �����ҽ���ֱ�ΪF1��F2��OΪԭ�㣮
�����ҽ���ֱ�ΪF1��F2��OΪԭ�㣮
 �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ ��
�� ��P��C�ϵĵ㣬
��P��C�ϵĵ㣬 ��
�� =
= ����C���������� ��
����C���������� ��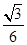 B��
B�� C��
C�� D��
D��
 �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ ��
�� ����
���� ����
����
 ��
�� ����ֱ��
����ֱ�� ����ԲC�ཻ��A��B���㣬��
����ԲC�ཻ��A��B���㣬��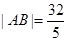 ��
��