题目内容
已知椭圆C:![]() 的左、右焦点为F1、F2,离心率为e. 直线
的左、右焦点为F1、F2,离心率为e. 直线![]() 与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
与x轴、y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设![]()
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() 的周长为6;写出椭圆C的方程.
的周长为6;写出椭圆C的方程.
(Ⅰ)见解析
(Ⅱ)![]()
解析:
(Ⅰ)证法一:因为A、B分别是直线![]() 轴、y轴的交点,
轴、y轴的交点,
所以A、B的坐标分别是![]() …………2分
…………2分
由 …………4分
…………4分
所以点M的坐标是![]()
即  ………………6分
………………6分
证法二:因为A、B分别是直线![]() 轴、y轴的交点,所以A、B的坐标分别是
轴、y轴的交点,所以A、B的坐标分别是![]() ………………2分
………………2分
设M的坐标是![]()
 ………………4分
………………4分
因为点M在椭圆上,所以 ![]()
即 
![]() …………6分
…………6分
(Ⅱ)当![]() 的周长为6,得
的周长为6,得![]()
所以![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 (2013•临沂二模)
(2013•临沂二模) 的左、右焦点分别为F1,F2,O为原点.
的左、右焦点分别为F1,F2,O为原点.
 的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线
的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线 相切.
相切. 的对称点,动点M满足
的对称点,动点M满足 . 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由.
. 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由. 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,点A是椭圆上任一点,
,点A是椭圆上任一点, 的周长为
的周长为 .
. 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于 两点,记
两点,记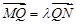 ,若在线段
,若在线段 上取一点R,使得
上取一点R,使得 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
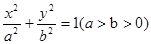 的左、右顶点的坐标分别为
的左、右顶点的坐标分别为 ,
, ,离心率
,离心率 。
。 ,
, ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两点,证明直线
两点,证明直线 与直线
与直线 的交点在直线
的交点在直线 上。
上。