题目内容
知椭圆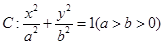 的离心率为
的离心率为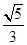 ,定点
,定点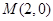 ,椭圆短轴的端点是
,椭圆短轴的端点是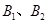 ,且
,且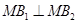 .
.
(1)求椭圆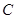 的方程;
的方程;
(2)设过点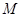 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆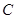 于
于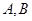 两点.试问
两点.试问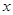 轴上是否存在异于
轴上是否存在异于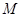 的定点
的定点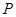 ,使
,使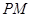 平分
平分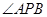 ?若存在,求出点
?若存在,求出点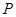 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
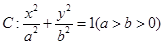 的离心率为
的离心率为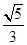 ,定点
,定点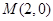 ,椭圆短轴的端点是
,椭圆短轴的端点是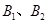 ,且
,且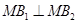 .
.(1)求椭圆
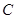 的方程;
的方程;(2)设过点
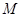 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆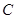 于
于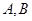 两点.试问
两点.试问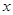 轴上是否存在异于
轴上是否存在异于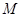 的定点
的定点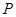 ,使
,使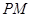 平分
平分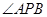 ?若存在,求出点
?若存在,求出点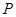 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.(1) ;(2)存在,
;(2)存在, .
.
 ;(2)存在,
;(2)存在, .
.试题分析:(1)由离心率为
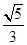 可得到一个关于
可得到一个关于 的方程,再根据MB1⊥MB2即可得
的方程,再根据MB1⊥MB2即可得 ;(2)本题采用“设而不求”的方法,将A,B两点坐标设出,但不求出.注意到
;(2)本题采用“设而不求”的方法,将A,B两点坐标设出,但不求出.注意到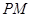 平分
平分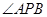 ,则直线
,则直线 的倾斜角互补这个性质,从而由斜率着手,以韦达定理为辅助工具,得出点P的坐标.
的倾斜角互补这个性质,从而由斜率着手,以韦达定理为辅助工具,得出点P的坐标.试题解析:(1)由
 得
得
又
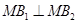 ,知
,知 是等腰直角三角形,从而
是等腰直角三角形,从而 .
.所以椭圆C的方程是
 . 5分
. 5分(2)设
 ,直线AB的方程为
,直线AB的方程为
由
 得
得 ,
,所以
 ①,
①,
 ② 8分
② 8分若
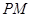 平分
平分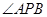 ,则直线
,则直线 的倾斜角互补,
的倾斜角互补,所以

设
 ,则有
,则有 , 10分
, 10分将
 代入上式,整理得
代入上式,整理得 ,
,将①②代入得
 ,由于上式对任意实数都成立,所以
,由于上式对任意实数都成立,所以 .
.综上,存在定点
 ,使平分PM平分∠APB. 13分
,使平分PM平分∠APB. 13分
练习册系列答案
相关题目
 时,求k的值.
时,求k的值. 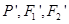 ,求以
,求以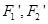 为焦点且过
为焦点且过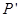 点的双曲线的标准方程。
点的双曲线的标准方程。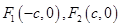 分别是椭圆
分别是椭圆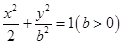 的左、右焦点,椭圆的离心率
的左、右焦点,椭圆的离心率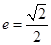 .
.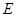 的方程;(II)已知直线
的方程;(II)已知直线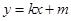 与椭圆
与椭圆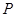 ,且与直线
,且与直线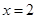 相交于点
相交于点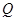 .求证:以线段
.求证:以线段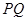 为直径的圆恒过定点
为直径的圆恒过定点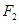 .
.
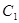 ,求证:O、
,求证:O、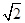 ,则P="__________" .
,则P="__________" .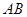 的两个端点在抛物线
的两个端点在抛物线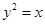 上滑动,则线段
上滑动,则线段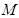 到
到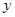 轴距离的最小值是
轴距离的最小值是 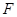 是抛物线
是抛物线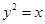 的焦点,
的焦点,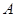 、
、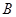 是该抛物线上的两点,且
是该抛物线上的两点,且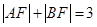 ,则线段
,则线段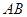 的中点到
的中点到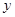 轴的距离为( )
轴的距离为( )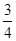
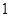
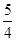
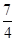
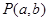 与点
与点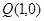 在直线
在直线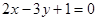 的两侧,则下列说法:
的两侧,则下列说法: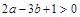 ;
;  时,
时,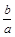 有最小值,无最大值;
有最小值,无最大值;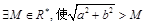 恒成立
恒成立 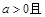
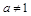 ,
,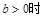 , 则
, 则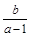 的取值范围为(-
的取值范围为(-