题目内容
6.过抛物线x2=2py(p>0)的焦点F作倾斜角为45°的直线,与抛物线分别交于A、B两点(A在y轴左侧),则$\frac{{|{AF}|}}{{|{FB}|}}$=$3-2\sqrt{2}$.分析 点斜式设出直线l的方程,代入抛物线方程,求出A,B两点的纵坐标,利用抛物线的定义得出$\frac{{|{AF}|}}{{|{FB}|}}$=$\frac{{y}_{1}+\frac{p}{2}}{{y}_{2}+\frac{p}{2}}$,即可得出结论.
解答 解:设直线l的方程为:x=y-$\frac{p}{2}$,A(x1,y1),B(x2,y2),
由x=y-$\frac{p}{2}$,代入x2=2py,可得y2-3py+$\frac{1}{4}$p2=0,
∴y1=$\frac{3-2\sqrt{2}}{2}$p,y2=$\frac{3+2\sqrt{2}}{2}$p,
从而,$\frac{{|{AF}|}}{{|{FB}|}}$=$\frac{{y}_{1}+\frac{p}{2}}{{y}_{2}+\frac{p}{2}}$=$3-2\sqrt{2}$.
故答案为:$3-2\sqrt{2}$.
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,利用抛物线的定义,得出$\frac{{|{AF}|}}{{|{FB}|}}$=$\frac{{y}_{1}+\frac{p}{2}}{{y}_{2}+\frac{p}{2}}$是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
17.在△ABC中,AB=2,AC=3,$BC=\sqrt{10}$,则△ABC的面积为( )
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\sqrt{15}$ | C. | $\frac{{3\sqrt{15}}}{4}$ | D. | $\frac{{3\sqrt{6}}}{16}$ |
14.在△ABC中,b=3,c=4,B=30°,则此三角形解的情况是( )
| A. | 一解 | B. | 两解 | C. | 一解或两解 | D. | 无解 |
11.定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0.则( )
| A. | $f({0.7^6})<f({log_{0.7}}6)<f({6^{0.5}})$ | B. | f(0.76)<f(60.5)<f(log0.76) | ||
| C. | $f({log_{0.7}}6)<f({0.7^6})<f({6^{0.5}})$ | D. | $f({log_{0.7}}6)<f({6^{0.5}})<f({0.7^6})$ |
18.函数$f(x)=\sqrt{{x^2}-2x-8}$的定义域为A,函数$g(x)=\frac{1}{{\sqrt{1-|{x-a}|}}}$的定义域为B,则使A∩B=∅的实数a的取值范围是( )
| A. | {a|-1<a<3} | B. | {a|-2<a<4} | C. | {a|-2≤a≤4} | D. | {a|-1≤a≤3} |




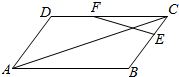 如图,在?ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{CE}$=$\frac{1}{3}$$\overrightarrow{CB}$,$\overrightarrow{CF}$=$\frac{2}{3}$$\overrightarrow{CD}$.
如图,在?ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{CE}$=$\frac{1}{3}$$\overrightarrow{CB}$,$\overrightarrow{CF}$=$\frac{2}{3}$$\overrightarrow{CD}$.