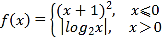题目内容
【题目】已知直线![]() 的方程为
的方程为![]() ,若
,若![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,且
,且![]() .
.
(1)求直线![]() 和
和![]() 的交点坐标;
的交点坐标;
(2)已知直线![]() 经过
经过![]() 与
与![]() 的交点,且在
的交点,且在![]() 轴上截距是在
轴上截距是在![]() 轴上的截距的2倍,求
轴上的截距的2倍,求![]() 的方程.
的方程.
【答案】(1)交点为![]() ;(2)
;(2)![]() 的方程为
的方程为![]() 或
或![]()
【解析】
(1)根据两直线垂直的关系,以及直线![]() 在
在![]() 轴上的截距,可得
轴上的截距,可得![]() 方程,联立方程,可得结果.
方程,联立方程,可得结果.
(2)利用(1)的结论,采用分类讨论的方法,可假设直线![]() 的截距式,利用(1)的结论,可得结果.
的截距式,利用(1)的结论,可得结果.
(1)由直线![]() 的方程为
的方程为![]() 且
且![]()
可得直线![]() 的斜率为:2,
的斜率为:2,
又![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,即过点
,即过点![]()
所以直线![]() 方程:
方程:![]()
即![]() ,
,
联立![]() 方程,得:
方程,得:
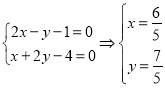 ,
,
故交点为![]()
(2)依据题意可知:
直线![]() 在
在![]() 轴上截距是在
轴上截距是在![]() 轴上的截距的2倍,
轴上的截距的2倍,
且直线![]() 经过
经过![]() 与
与![]() 的交点
的交点![]()
当直线![]() 原点时,
原点时,![]() 方程为:
方程为:![]()
当直线![]() 不过原点时,设
不过原点时,设![]() 方程为
方程为![]()
则![]() ,故
,故![]() 方程为:
方程为:![]() ,
,
即![]()
综上所述:
![]() 的方程为
的方程为![]() 或
或![]()

练习册系列答案
相关题目
【题目】某糕点房推出一类新品蛋糕,该蛋糕的成本价为4元,售价为8元.受保质期的影响,当天没有销售完的部分只能销毁.经过长期的调研,统计了一下该新品的日需求量.现将近期一个月(30天)的需求量展示如下:
日需求量x(个) | 20 | 30 | 40 | 50 |
天数 | 5 | 10 | 10 | 5 |
(1)从这30天中任取两天,求两天的日需求量均为40个的概率.
(2)以上表中的频率作为概率,列出日需求量![]() 的分布列,并求该月的日需求量
的分布列,并求该月的日需求量![]() 的期望.
的期望.
(3)根据(2)中的分布列求得当该糕点房一天制作35个该类蛋糕时,对应的利润的期望值为![]() ;现有员工建议扩大生产一天45个,求利用利润的期望值判断此建议该不该被采纳.
;现有员工建议扩大生产一天45个,求利用利润的期望值判断此建议该不该被采纳.