题目内容

已知点A（1，1）而且F1是椭圆
x2
9
+
y2
5
=1的左焦点，P是椭圆上任意一点，求|PF1|+|PA|的最大值和最小值．
考点：椭圆的应用
专题：综合题,圆锥曲线的定义、性质与方程
分析：|PF1|+|PF2|=2a=6，|PF1|=6-|PF2|，所以，|PF1|+|PA|=6-|PF2|+|PA|=6+（|PA|-|PF2|），由此结合图象能求出|PF1|+|PA|的最小值．
解答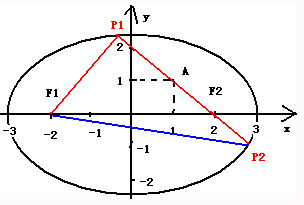： 解：∵|PF1|+|PF2|=2a=6
∴|PF1|=6-|PF2|
∴|PF1|+|PA|=6-|PF2|+|PA|=6+（|PA|-|PF2|）
当点P位于P1时，|PA|-|PF2|的差最小，其值为-|AF2|=-
2
此时，|PF1|+|PA|也得到最小值，其值为6-
2
；
当点P位于P2时，|PA|-|PF2|的差最大，其值为|AF2|=
2
此时，|PF1|+|PA|也得到最大值，其值为6+
2
．
点评：本题考查椭圆的性质和应用，考查椭圆的定义，解题时要注意数形结合法的合理运用．
练习册系列答案
相关题目
若P={x|x＜1}，Q={x|x＞-1}，则（　　）
A、∁RP⊆Q
B、Q⊆P
C、P⊆Q
D、Q⊆∁RP
已知椭圆的焦距是8，椭圆上任意一点到两焦点F1、F2的距离之和为10．
（1）求椭圆方程；
（2）在（1）的椭圆上求一点P，使PF1⊥PF2．
已知f（
x-1
x+1
）=
x2-1
x2+1
，求f（x）的解析式．
已知{an}是等差数列，公差为d，首项a1=3，前n项和为Sn．令cn=(-1)nSn(n∈N*)，{cn}的前20项和T20=330．数列{bn}满足bn=2（a-2）dn-2+2n-1，a∈R．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若bn+1≤bn，n∈N*，求a的取值范围．
若椭圆上存在一点P，它到椭圆中心和长轴一个端点的连线互相垂直，求椭圆离心率e的取值范围．
设函数f（x）=x+a
1-x
(a∈R)．
（1）若a=1，求f（x）的值域；
（2）若不等式f（x）≤2对x∈[-8，-3]恒成立，求实数a的取值范围．
已知f（x）=x+
1
|x|
．
（1）指出的f（x）值域；
（2）求函数g（x）=f（x）-p（p∈R）的零点的个数．
（3）若函数f（x）对任意x∈[-2，-1]，不等式f（mx）+mf（x）＜0恒成立，求实数m的取值范围．
已知（x+1）2+（y+1）2≤4，则2x-y的最大值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网