题目内容
如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=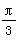 ,且△PF1F2的面积为2
,且△PF1F2的面积为2 ,又双曲线的离心率为2,求该双曲线的方程.
,又双曲线的离心率为2,求该双曲线的方程.

解:设双曲线方程为: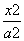 -
-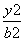 =1(a>0,b>0),
=1(a>0,b>0),
F1(-c,0),F2(c,0),P(x0,y0).
在△PF1F2中,由余弦定理,得:
|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cos
=(|PF1|-|PF2|)2+|PF1|·|PF2|,
即4c2=4a2+|PF1|·|PF2|,
又∵S△PF1F2=2 ,
,
∴ |PF1|·|PF2|·sin
|PF1|·|PF2|·sin 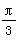 =2
=2 ,
,
∴|PF1|·|PF2|=8 .
.
∴4c2=4a2+8,即b2=2.
又∵e= =2,∴a2=
=2,∴a2= ,
,
∴双曲线的方程为: -
- =1.
=1.

练习册系列答案
相关题目
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
| 年份 | 2004 | 2006 | 2008 | 2010 | 2012[ |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量与年份之间的回归直线方程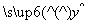 =bx+a;
=bx+a;
(2)利用(1)中所求出的直线方程预测该地2014年的粮食需求量.
 分,使得这两部分的面积之差最大,则该直线的方程为( )
分,使得这两部分的面积之差最大,则该直线的方程为( )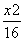 -
-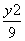 =1 B.
=1 B.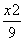 -
-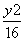 =1
=1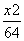 -
-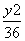 =1 D.
=1 D.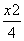 -
-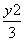 =1
=1 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 >2(其中O为原点),求k的取值范围.
>2(其中O为原点),求k的取值范围.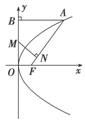
 的展开式中
的展开式中 项的系数是( A )
项的系数是( A ) B.
B. C.
C. D.
D.