题目内容
已知中心在原点的双曲线C的右焦点为(2,0),右顶点为( ,0).
,0).
(1)求双曲线C的方程;
(2)若直线l:y=kx+ 与双曲线C恒有两个不同的交点A和B,且
与双曲线C恒有两个不同的交点A和B,且 >2(其中O为原点),求k的取值范围.
>2(其中O为原点),求k的取值范围.
解:(1)设双曲线C的方程为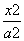 -
-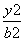 =1(a>0,b>0).
=1(a>0,b>0).
由已知得a= ,c=2,再由c2=a2+b2得b2=1,
,c=2,再由c2=a2+b2得b2=1,
所以双曲线C的方程为 -y2=1.
-y2=1.
(2)将y=kx+ 代入
代入 -y2=1中,
-y2=1中,
整理得(1-3k2)x2-6 kx-9=0,
kx-9=0,
由题意得 ,
,
故k2≠ 且k2<1.①
且k2<1.①
设A(xA,yA),B(xB,yB),则
 xAxB+yAyB=xAxB+(kxA+
xAxB+yAyB=xAxB+(kxA+ )(kxB+
)(kxB+ )=(k2+1)xAxB+
)=(k2+1)xAxB+ k(xA+xB)+2=(k2+1)·
k(xA+xB)+2=(k2+1)· , 解得
, 解得 <k2<3.②
<k2<3.②
由①②得 <k2<1,
<k2<1,
所以k的取值范围为

练习册系列答案
相关题目
 B.2
B.2 D.0
D.0 中,直线3x+4y-5=0与圆x2+y2=4相交于A、B两点,则弦AB的长等于( )
中,直线3x+4y-5=0与圆x2+y2=4相交于A、B两点,则弦AB的长等于( ) B.2
B.2 =1表示焦点在x轴上的双曲线的充要条件是( )
=1表示焦点在x轴上的双曲线的充要条件是( ) <-3或k>-2 D.k>-2
<-3或k>-2 D.k>-2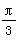 ,且△PF1F2的面积为2
,且△PF1F2的面积为2
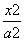 +
+ =1(a>b>0)的左、右焦点,P为直线x=
=1(a>b>0)的左、右焦点,P为直线x= 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( ) B.
B.
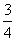 D.
D.
 离心率为
离心率为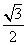 .双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )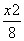 +
+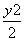 =1 B.
=1 B.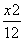 +
+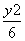 =1
=1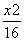 +
+ =1 D.
=1 D.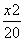 +
+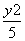 =1
=1 2x的焦点为F,过点M(
2x的焦点为F,过点M(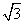 ,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于点C,BF=2,则△BCF与△ACF的面积之比为________.
,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于点C,BF=2,则△BCF与△ACF的面积之比为________.



 个等式应为
个等式应为