题目内容
根据要求证明下列各题：
（1）用分析法证明：
（2）用反证法证明：1，
，3不可能是一个等差数列中的三项
（1）详见解析，（2）详见解析.
解析试题分析：（1）分析法证明，从所求证结论出发，找出其成立的必要条件，直至这个条件为已知条件或恒成立条件. 要证：；即证：
即证：
即证：
即证：
；即证：
；而显然成立，且以上各步皆可逆,所以：,（2）反证法用于直接证明结论比较困难或繁琐，而其反面较简单的情况.注意反设是要全面、正确. 假设1，，3是某一个等差数列中的三项，且分别是第
项（
），
则数列的公差
，则
，因为，所以
，所以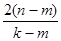
为有理数，所以
是有理数，这与是无理数相矛盾. 故假设不成立，所以1，，3不可能是某等差数列的三项.
试题解析：（1）要证：
；即证：
；
即证：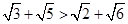
；即证：
；
即证：
；即证：
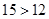；而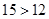显然成立，且以上各步皆可逆，
所以： 7分
（其他方法参照给分）
（2）假设1，
，3是某一个等差数列中的三项，且分别是第项（
）， 9分
则数列的公差
，则
，
因为，所以
，所以
为有理数， 12分
所以
是有理数，这与是无理数相矛盾。
故假设不成立，所以1，，3不可能是某等差数列的三项。 14分
考点：分析法及反证法
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
，则
.
的前
项和为
，且满足
．
，
，
，
的值并写出其通项公式；
；
均为实数，且
，
，
，求证
<a<c＋
,…,计算得
,….由此可猜测
=