题目内容
⑴用综合法证明: ;
;
⑵用反证法证明:若 均为实数,且
均为实数,且 ,
, ,
, ,求证
,求证 中至少有一个大于0.
中至少有一个大于0.
(1)详见解析,(2)详见解析.
解析试题分析:(1)综合法证明,实质先按分析法分析,再按综合法的写法. 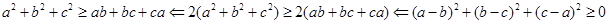 (2)反证法证明,关键在于正确假设:假设
(2)反证法证明,关键在于正确假设:假设 都不大于0,则
都不大于0,则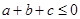 ,又
,又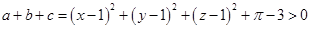 ,两者矛盾,故假设错误。从而中至少有一个大于0.
,两者矛盾,故假设错误。从而中至少有一个大于0.
(1)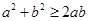 ①
①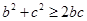 ②
②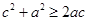 ③
③
①+②+③得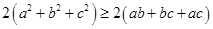
即
当且仅当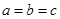 时,取“=”
时,取“=”
(2)假设 都不大于0
都不大于0
则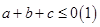
又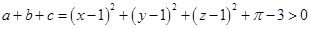
与(1)式矛盾,故假设错误
从而 中至少有一个大于0
中至少有一个大于0
考点:综合法,反证法

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知二次函数f(x)=ax2+bx+c的图象与x轴有两个不同的交点,若f(c)=0且0<x<c时,f(x)>0,
(1)证明: 是f(x)=0的一个根;
是f(x)=0的一个根;
(2)试比较 与c的大小;
与c的大小;
(3)证明:-2<b<-1.
设 是由
是由 个实数组成的
个实数组成的 行
行 列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”.
(Ⅰ) 数表 如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实数,请写出每次“操作”后所得的数表(写出一种方法即可);
表1
| 1 | 2 | 3 |  |
 | 1 | 0 | 1 |
(Ⅱ) 数表
 如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数
如表2所示,若经过任意一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数 的所有可能值;
的所有可能值;表2
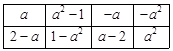
(Ⅲ)对由
 个整数组成的
个整数组成的 行
行 列的任意一个数表
列的任意一个数表 ,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由.
,能否经过有限次“操作”以后,使得到的数表每行的各数之和与每列的各数之和均为非负整数?请说明理由. 
 ,3不可能是一个等差数列中的三项
,3不可能是一个等差数列中的三项 为三角形
为三角形 的三边,求证:
的三边,求证:
 中,
中, ,且
,且 成等差数列,
成等差数列, 成等比数列
成等比数列 .
. ;
; 使得
使得 对一切
对一切 恒成立?若存在,求出
恒成立?若存在,求出 ,
, ,
, ,
, ,
, ,你能得到一个怎样的一般不等式?并加以证明.
,你能得到一个怎样的一般不等式?并加以证明. ”时,某同学学到了如下一种方法:
”时,某同学学到了如下一种方法: 由此得
由此得



 ”,其结果为
”,其结果为