题目内容
16.对一质点的运动过程观测了4次,得到如表所示的数据,| x | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 6 |
(2)求回归方程.
分析 (1)根据所给的四对数据,做出y与x的平均数,即样本点的中心;
(2)把所求的平均数代入求$\widehat{b}$的公式,做出它的值,再把它代入求a的式子,求出a的值,根据做出的结果,写出线性回归方程.
解答 解:(1)将给出的数据代入公式求解,可求得:
$\overline{x}$=$\frac{1}{4}$(1+2+3+4)=2.5,$\overline{y}$=$\frac{1}{4}$(1+3+5+6)=3.75,
故样本点的中心是(2.5,3.75);
(2)由(1)$\widehat{b}$=$\frac{46-4×2.5×3.75}{30-4×2.52}$=1.7,
$\widehat{a}$=$\overline{y}$-$\widehat{b}$•$\overline{x}$=-0.5,
∴所求回归直线方程为$\widehat{y}$=1.7x-0.5.
点评 在一组具有相关关系的变量的数据间,通过散点图可观察出所有数据点都分布在一条直线附近,这样的直线可以画出许多条,而其中的一条能最好地反映x与Y之间的关系,这就是回归直线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.方程$(x+y-1)\sqrt{{x^2}+{y^2}-4}=0$所表示的图形是( )
| A. | 两条射线及一个圆 | B. | 两个点 | ||
| C. | 一条线段及一个圆 | D. | 一条直线及一个圆 |
11.某程序框图如图所示,运行该程序输出的k值是( )
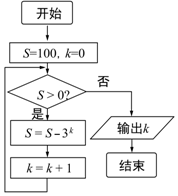

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
4.已知奇函数f(x)=ax5+bx4+cx3+dx2+ex+f单调递减,且满足f(f(x))=x,那么f(1)-f(-1)=( )
| A. | -2 | B. | -4 | C. | -8 | D. | 不能确定 |
8.已知一个数列的前n项和为Sn=3n2+2n+5,则它的第n(n≥2)项为( )
| A. | 3n2 | B. | 3n2+3n | C. | 6n+1 | D. | 6n-1 |