题目内容
 的最小值是( )
的最小值是( )
| A.2 | B. | C.5 | D.8 |
C.
解析试题分析:因为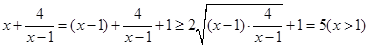 .当且仅当x=3或x=-1.所以选C.基本不等式的应用要注意“一正二定三相等”.由于x>1,所以x-1>0.并且要验证等号成立时是否取得到.
.当且仅当x=3或x=-1.所以选C.基本不等式的应用要注意“一正二定三相等”.由于x>1,所以x-1>0.并且要验证等号成立时是否取得到.
考点:基本不等式的应用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
若a、b∈R,且ab>0,则下列不等式中,恒成立的是( ).
| A.a2+b2>2ab | B.a+b≥2 |
C. | D. |
函数 的最大值是( )
的最大值是( )
A. | B.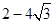 | C. | D. |
下列函数中,当 取正数时,最小值为
取正数时,最小值为 的是 ( )
的是 ( )
A. | B. |
C. | D. |
若 且
且 ,使不等式
,使不等式 ≥
≥ 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. ≤ ≤ | B. ≤ ≤ | C. ≥ ≥ | D. ≥ ≥ |
设 为坐标原点,第一象限内的点
为坐标原点,第一象限内的点 的坐标满足约束条件
的坐标满足约束条件 ,
, ,若
,若 的最大值为40,则
的最大值为40,则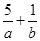 的最小值为( )
的最小值为( )
A. | B. | C.1 | D.4 |
对于实数 和
和 ,定义运算
,定义运算 :
: ,若对任意
,若对任意 ,不等式
,不等式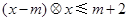 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是
A. | B.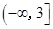 |
C.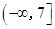 | D. |
若直线ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则 +
+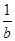 的最小值为( )
的最小值为( )
A. | B. |
C. + + | D. +2 +2 |
 ,得2分的概率为
,得2分的概率为 ,不得分的概率为
,不得分的概率为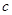 ,
, ,已知他投篮一次得分的期望是2,则
,已知他投篮一次得分的期望是2,则 的最小值为( )
的最小值为( )


