题目内容
已知点P是以F1、F2为焦点的椭圆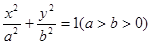 上一点,且
上一点,且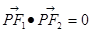 ,
,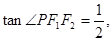 则该椭圆的离心率为( )
则该椭圆的离心率为( )
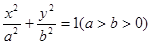 上一点,且
上一点,且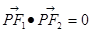 ,
,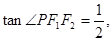 则该椭圆的离心率为( )
则该椭圆的离心率为( )A.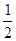 | B.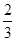 | C.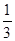 | D.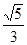 |
D
试题分析:设
 ,因为
,因为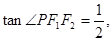 ,所以
,所以 ,由椭圆的定义知:
,由椭圆的定义知: ,又因为
,又因为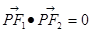 ,所以
,所以 ,所以该椭圆的离心率为
,所以该椭圆的离心率为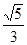 。
。点评:求圆锥曲线的离心率是常见题型,常用方法:①直接利用公式
 ;②利用变形公式:
;②利用变形公式: (椭圆)和
(椭圆)和 (双曲线)③根据条件列出关于a、b、c的关系式,两边同除以a,利用方程的思想,解出
(双曲线)③根据条件列出关于a、b、c的关系式,两边同除以a,利用方程的思想,解出 。
。
练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 ,曲线
,曲线 .自曲线
.自曲线 上一点
上一点 作
作 的两条切线切点分别为
的两条切线切点分别为 .
.
 ,求
,求 ;
; 的最大值.
的最大值.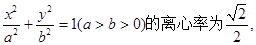 其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=
其左、右焦点分别为F1、F2,点P是坐标平面内一点,且|OP|=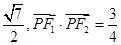 (O为坐标原点)。
(O为坐标原点)。 l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。
l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点:若存在,求出M的坐标;若不存在,说明理由。 有相同的长度单位,以原点
有相同的长度单位,以原点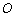 为极点,以
为极点,以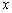 正半轴为极轴,已知曲线
正半轴为极轴,已知曲线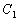 的极坐标方程为
的极坐标方程为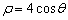 ,曲线
,曲线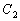 的参数方程是
的参数方程是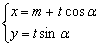 (
(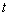 为参数,
为参数,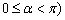 ,射线
,射线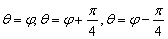 与曲线
与曲线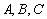
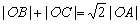 ;
;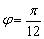 时,
时,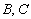 两点在曲线
两点在曲线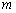 与
与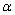 的值.
的值.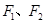 ,且两条曲线在第一象限的交点为
,且两条曲线在第一象限的交点为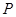 ,
,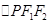 是以
是以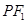 为底边的等腰三角形,若
为底边的等腰三角形,若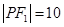 ,椭圆与双曲线的离心率分别为
,椭圆与双曲线的离心率分别为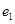 ,
,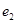 ,则
,则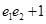 的取值范围是( )
的取值范围是( )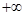 )
)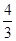 ,
,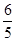 ,
,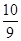 ,+
,+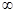 )
)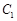 的极坐标方程是
的极坐标方程是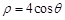 ,以极点为原点,极轴为
,以极点为原点,极轴为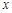 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: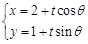 (为参数).
(为参数).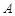 ,
,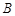 两点,点
两点,点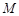 的直角坐标为
的直角坐标为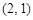 ,若
,若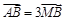 ,求直线的普通方程.
,求直线的普通方程.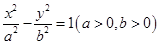 的左焦点
的左焦点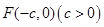 ,作倾斜角为
,作倾斜角为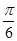 的直线FE交该双曲线右支于点P,若
的直线FE交该双曲线右支于点P,若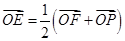 ,且
,且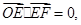 则双曲线的离心率为( )
则双曲线的离心率为( )
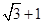

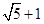
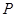 是双曲线
是双曲线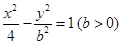 上一点,
上一点,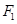 、
、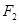 是其左、右焦点,
是其左、右焦点,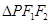 的三边长成等差数列,且
的三边长成等差数列,且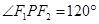 ,则双曲线的离心率等于
,则双曲线的离心率等于
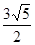
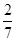
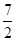
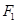 ,
,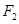 是椭圆
是椭圆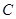 的两个焦点,焦距为4.若
的两个焦点,焦距为4.若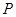 为椭圆
为椭圆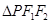 的周长为14,则椭圆
的周长为14,则椭圆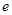 为______________
为______________