题目内容
已知矩形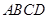
的顶点都在半径为4的球
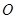的球面上，且
，
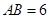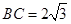，则棱锥
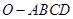的体积为 .
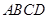的顶点都在半径为4的球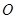的球面上，且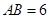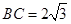，，则棱锥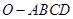的体积为 .
试题分析：根据体积公式，应求出矩形
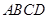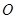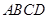的面积和球心到底面的距离
.矩形
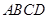的外接圆的半径
，所以
，体积
.
的应用.
练习册系列答案
相关题目
试题分析：根据体积公式，应求出矩形
的面积和球心到底面的距离.矩形
的外接圆的半径，所以，体积
.的应用.题目内容
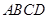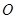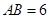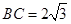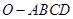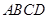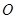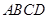的顶点都在半径为4的球的球面上，且，，则棱锥的体积为 .的面积和球心到底面的距离.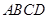的外接圆的半径，所以，.的应用.
,AA1=3,E为CD上一点,DE=1,EC=3
到平面EA1C1的距离.
B． 
C．
D．
，且体对角线与底面所成角的余弦值为
，则该正四棱柱的体积等于 ．
，则该正四棱锥的外接球的表面积为 .
中，
，
，
， 
，
，
和
分别是
和
的中点.
底面
；
平面
；
的体积.
的棱长为6，则以正方体
截正方体外接球所得的圆为底面的圆锥的表面积为__________