题目内容
P是正方形ABCD所在平面外一点,且PA=PB=PC=PD=AB=13,M、N分别是PA与BD上的点,且
.(1)求证:MN∥平面PBC;
(2)求线段MN的长.
解析:在面PBC内找一条直线,使这条直线与MN平行.
(1)证明:过M、N分别在平面PAB和平面ABCD内作MH∥AB交PB于H,作NK∥DC交BC于K,
则由AB∥DC知MH∥NK.
由,
故
.
又AB=DC,知NK=MH,故四边形NKHM是平行四边形,得MN∥HK.
又MN平面PBC,HK
平面PBC,故MN∥平面PBC.
(2)解:由已知,可得△PBC为正三角形,据(1),知BK=5,BH=8,∠PBC=60°,
故HK=
=7,即MN=7.
小结:（1）利用AB∥DC推得MH∥NK,利用
推得MH=NK,从而得到四边形MNKH为平行四边形，进一步证得MN∥平面PBC;（2）用余弦定理求出的HK的值即为MN的值.
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
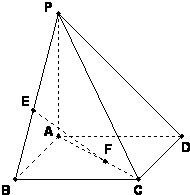如图，已知点P是正方形ABCD所在平面外一点，PA⊥平面ABCD，PA=AB，点E、F分别在线段PB、AC上，满足BE=CF．
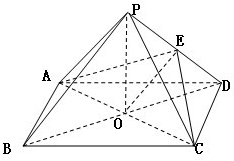如图：已知P是正方形ABCD所在平面外一点，点P在平面ABCD内的射影O是正方形的中心，PO=OD=a，E是PD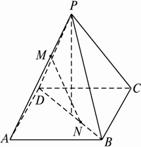的中点
平面ABCD，PA=AB=2，且E、F分别是AB、PC的中点.