题目内容
如图,点P是正方形ABCD外一点,PA 平面ABCD,PA=AB=2,且E、F分别是AB、PC的中点.
平面ABCD,PA=AB=2,且E、F分别是AB、PC的中点.
(1)求证:EF//平面PAD;
(2)求证:EF 平面PCD;
平面PCD;
(3)求:直线BD与平面EFC所成角的大小.

【答案】
(1)取PD中点M,连结AM,FM
由FM//CD,FM= CD,得FM//AE,FM=AE,
CD,得FM//AE,FM=AE, 四边形AEFM是平行四边形
四边形AEFM是平行四边形
 EF//AM,又AM
EF//AM,又AM 面PAD,
面PAD, EF//面PAD
EF//面PAD
(2) PA
PA 面ABCD
面ABCD  PA
PA CD,又AD
CD,又AD CD
CD
 CD
CD 面PAD
面PAD  AM
AM CD
CD
又 PA=AB=2
PA=AB=2  AM
AM PD
PD  AM
AM 面PCD
面PCD  EF
EF 面PCD
面PCD
(3)过点D作DN PC交于点N,设BD与EC交于点Q,连结QN
PC交于点N,设BD与EC交于点Q,连结QN
由(2)知 DQN为所求角
DQN为所求角  DN=
DN= ,DQ=
,DQ=
 Rt
Rt DNQ中,sin
DNQ中,sin  DQN=
DQN= =
=

 DQN=
DQN=
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图:点P在正方形ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题:
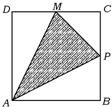
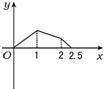
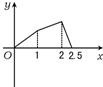
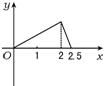
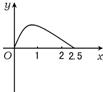
如图:点P在正方形ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题: 如图,点P在边长为1的正方形ABCD上运动,设点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM面积设为y,则函数y=f(x)的图象只可能是下图中的( )
如图,点P在边长为1的正方形ABCD上运动,设点M为CD的中点,当点P沿A→B→C→M运动时,点P经过的路程设为x,△APM面积设为y,则函数y=f(x)的图象只可能是下图中的( ) (2013•日照一模)如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中
(2013•日照一模)如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中 如图:点P在正方形ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题:
如图:点P在正方形ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题: