题目内容
已知P是正方形ABCD所在平面外一点,PB⊥平面ABCD,PB=BC,则PC与BD所成的角为
60°
60°
.分析:直接由题意建立空间直接坐标系,设出PB=BC=1,求出PC与BD对应向量的坐标,利用两向量夹角的余弦值求夹角,从而得到两条异面直线所成的角.
解答: 解:如图,
解:如图,
由题意,以B为坐标原点,分别以BC、BA、BP所在直线为x、y、z轴建立空间直角坐标系.
设PB=BC=1,则B(0,0,0),D(1,1,0),C(1,0,0),P(0,0,1).
=(1,0,-1),
=(1,1,0).
∴cos<
,
>=
=
=
.
∴PC与BD所成的角为60°.
故答案为60°.
 解:如图,
解:如图,由题意,以B为坐标原点,分别以BC、BA、BP所在直线为x、y、z轴建立空间直角坐标系.
设PB=BC=1,则B(0,0,0),D(1,1,0),C(1,0,0),P(0,0,1).
| PC |
| BD |
∴cos<
| PC |
| BD |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
∴PC与BD所成的角为60°.
故答案为60°.
点评:本题考查了空间异面直线所成角的大小,考查了利用空间向量求异面直线所成的角,关键是注意异面直线所成角的范围,是中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.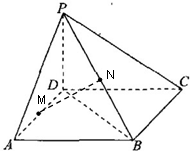 已知四棱锥P-ABCD的底面ABCD是正方形,M,N分别为AD,PB的中点,且PD⊥底面ABCD,其中PD=AD=a.
已知四棱锥P-ABCD的底面ABCD是正方形,M,N分别为AD,PB的中点,且PD⊥底面ABCD,其中PD=AD=a.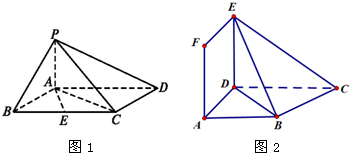
 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.