题目内容
已知A={|x-1|＜m,m＞0},B={x||x-3|＞4},且A∩B=
.求实数m的取值范围.
解：由|x-1|＜m,m＞0得-m＜x-1＜m,
∴1-m＜x＜m+1.
∴A={x|1-m＜x＜m+1,m＞0}.
由|x-3|＞4得x-3＞4或x-3＜-4,
∴x＞7或x＜-1.
∴B={x|x＜-1或x＞7}.
∵A∩B=,从数轴上分析出的m应满足
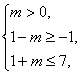
∴已知中的m＞0不能丢下，注意不等号的选择
∴0＜m≤2.
∴m的取值范围为{m|0＜m≤2}.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目