题目内容
若实数a>0,b>0,且a+b+
+
=10,则a+b最大值是
| 4 |
| a |
| 1 |
| b |
9
9
.分析:可令t=a+b,则0<t<10.于是a+b+
+
=10可转化为t+(
+
)(
)=10,即(10-t)t=(
+
)(a+b),展开后应用基本不等式即可.
| 4 |
| a |
| 1 |
| b |
| 4 |
| a |
| 1 |
| b |
| a+b |
| t |
| 4 |
| a |
| 1 |
| b |
解答:解:令t=a+b,则0<t<10,
=1,
∵a>0,b>0,a+b+
+
=10,
∴t+(
+
)(
)=10,
∴(10-t)t=(
+
)(a+b)=4+
+
+1≥9(当且仅当a=2b=6时取“=”),
∴t2-10t+9≤0,
∴1≤t≤9.
故答案为:9.
| a+b |
| t |
∵a>0,b>0,a+b+
| 4 |
| a |
| 1 |
| b |
∴t+(
| 4 |
| a |
| 1 |
| b |
| a+b |
| t |
∴(10-t)t=(
| 4 |
| a |
| 1 |
| b |
| 4b |
| a |
| a |
| b |
∴t2-10t+9≤0,
∴1≤t≤9.
故答案为:9.
点评:本题考查基本不等式在最值问题中的应用,关键在于令a+b=t进行换元,难点在于对已知条件a+b+
+
=10的转化(化为t+(
+
)(
)=10),属于难题.
| 4 |
| a |
| 1 |
| b |
| 4 |
| a |
| 1 |
| b |
| a+b |
| t |

练习册系列答案
相关题目
 +
+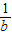 =10,则a+b最大值是 .
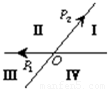
=10,则a+b最大值是 . ,且点P落在第Ⅲ部分,则实数a、b满足( )
,且点P落在第Ⅲ部分,则实数a、b满足( )
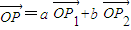 ,且点P落在第Ⅲ部分,则实数a、b满足( )
,且点P落在第Ⅲ部分,则实数a、b满足( )